freinage_cyclisme

Jacques Fine. Février 2016. Complété en 2019.
contact@velomath.fr
http://www.velomath.fr

Freiner est un geste extrêmement banal lors de la pratique du vélo. Il est très intuitif et l’action du cycliste sur les manettes de frein peut être exécutée de mille et une façons. Néanmoins cette action peut être mal menée et conduire à une chute.

Dans ce document, nous ne nous intéresserons pas à l’aspect technologique du système de freinage (freins à patins, à disque ou autres) mais nous considérons que nous avons affaire au système courant des vélos de route, c’est-à-dire des freins à patins.

Analyse qualitative.

La figure 1 illustre les forces en présence. On peut distinguer deux types de force :

Les forces motrices. Ce sont les forces qui provoquent le mouvement du cycliste.

force d’inertie Fi. Au moment où le cycliste décide de freiner, il arrête le pédalage et ne produit donc plus de force de pédalage. En revanche, étant donné qu’il roule à une certaine vitesse, il a emmagasiné de l’énergie qu’il libérera sous force d’énergie cinétique à partir du moment où il cesse le pédalage. Cette énergie diminuera avec la progression du cycliste et finira par s’annuler lorsque la vitesse sera nulle. L’énergie cinétique comprend une énergie de translation due au mouvement de translation du cycliste et une énergie cinétique de rotation due aux pièces en rotation, surtout les roues. Dans la suite de ce document, nous négligerons les forces d’inertie de rotation qui sont faibles par rapport à la force d’inertie de translation.
la force de pesanteur. Dans le problème de freinage, cette force est généralement une force motrice car, dans la plupart des cas, on freine dans une descente ou sur du plat et rarement en montant une cote. Dans ce dernier cas, la force de pesanteur devient une force résistante. La valeur de la force de pesanteur est la composante du poids cycliste-vélo suivant la pente de la route.

Les forces résistantes. Ce sont les forces qui doivent être vaincues par les forces motrices pour que le cycliste puisse avancer.

les forces de freinage. Pour freiner, le cycliste exerce des forces b1 et b2 sur les manettes de frein. Ces forces sont amplifiées par un effet de bras de levier au niveau des manettes et sont transmises par les câbles aux étriers de frein. A leur tour, les étriers transmettent un effort sur les patins avec également un effet de bras de levier qui peut être amplificateur ou parfois réducteur. Les patins exercent un effort sur la jante de la roue. Cet effort dit « normal », c’est-à-dire perpendiculaire à la surface de la jante, induit un effort dit « tangentiel » sur la jante grâce au frottement entre le patin et la jante. Cet effort tangentiel induit sur les roues « un couple de freinage ». La valeur de ce couple peut s’exprimer par des forces B1 et B2 s’exerçant au niveau du contact roue-chaussée qu’il faudra vaincre si l’on veut que les roues tournent.
les forces de frottement entre les roues et chaussée. Ces forces sont faibles, leur ordre de grandeur correspond aux forces de pesanteur qu’il faut vaincre en gravissant une pente de 1%.
la résistance de l’air. Cette force s’applique sur le cycliste et son vélo. On peut en avoir un bon ordre de grandeur par des tests simples décrits dans le document « Le vélo en équation ». On notera qu’il est difficile de préciser exactement le point d’application de cette force. Estimer que ce point est le centre de gravité G du cycliste est une hypothèse qui peut sembler raisonnable. On notera aussi qu’en cas de vent arrière dont la vitesse est supérieure à celle du cycliste, le cycliste est poussé par le vent et la force de résistance devient une force propulsive, donc une force motrice.

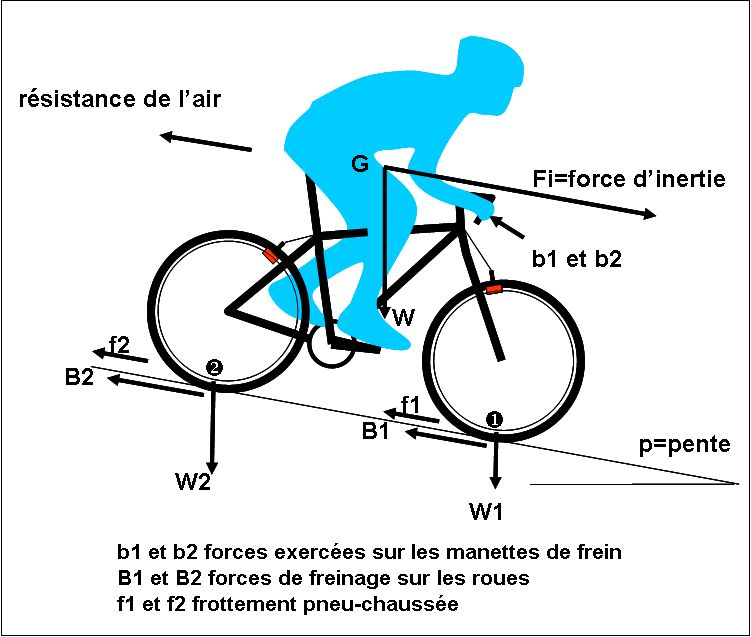
Fig.1. Les forces en présence

Sous l’effet de ces forces, le cycliste s’arrêtera lorsque les forces résistantes seront égales aux forces motrices.

Deux incidents peuvent néanmoins se produire :

le basculement du cycliste vers l’avant avec le risque de passer par-dessus le vélo. En effet, on peut voir sur la figure 1 que, si la force d’inertie est très importante, le couple exercé au point 1 (contact de la roue avant avec le sol) par la force motrice Fi peut être supérieur au couple exercé par la force résistante W2.
le blocage des roues. Cela peut survenir si les forces de freinage sont trop importantes. La ou les roues bloquées glisseront alors sur la chaussée sans tourner. Cela entraînera pour le cycliste la perte de maîtrise de la direction et souvent une chute.

Analyse quantitative

Dans cette première analyse, nous effectuerons un calcul global, sans différencier la roue avant et la roue arrière. Cette procédure est valable tant que l’on ne s’intéresse pas aux problèmes de glissement ou basculement.

Nous utiliserons les unités légales et non pas les unités familières aux cyclistes, contrairement à d’autres documents présentés sur ce site, et cela afin de ne pas alourdir les équations. Adoptons les notations suivantes :

W le poids cumulé du cycliste et du vélo en Newton. Il suffit de se souvenir qu’un poids de 1 kg correspond à 10 Newtons.
V la vitesse du cycliste en m/s. Il faut se souvenir que la vitesse en km/h s’obtient en multipliant par 3,6. Ainsi, 10 m/s correspond à 36 km/h.
V0 est la vitesse initiale au moment où le cycliste commence à freiner
B est la force de freinage en Newton (B=B1+B2)
i angle de pente de la chaussée. Etant donné que le freinage concerne surtout les descentes, par convention, nous adopterons une valeur positive de l’angle i pour des descentes
p la pente de la route. Elle est égale à tg i. On l’exprime en % dans le langage courant. Une pente de 4% est égale à 0,04. Par convention, la pente sera comptée positive pour une descente et donc négative pour une montée. car le freinage concerne plus les descentes que les montées.
f est le coefficient de frottement roues/chaussée (f est de l’ordre de 0,01).
Cx est le coefficient de pénétration dans l’air, de l’ordre de 0,20 à 0,25
l’unité de temps est la seconde
g est l’accélération de la pesanteur exprimée en m/s² et vaut 9,81 m/s²

L’équation du mouvement de translation du cycliste s’écrit :

masse x accélération = -force de pesanteur -force de frottement -résistance de l’air -force de freinage

soit :

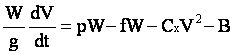
équation [1]

Il nous faut distinguer deux cas :

Premier cas : fort freinage B > W(p-f)

On posera :

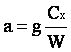
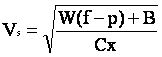
Avec ces notations, l’équation devient :

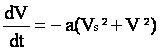
soit :

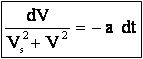équation [2]

La force de freinage B exercée par le cycliste peut être variable dans le temps. Celui-ci peut freiner progressivement ou bien freiner très fort puis relâcher progressivement la manette. Si B varie en fonction du temps, l’équation différentielle n’a pas de solution analytique mais on peut la résoudre numériquement cas par cas.

En revanche, si le cycliste exerce une force de freinage constante, l’équation a une solution analytique qui est présentée ci-après.

Si B est constant, l’intégration de l’équation différentielle [1] aboutit à :

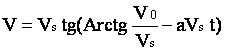
La distance parcourue x en fonction du temps est solution de l’équation différentielle :

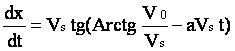
Compte tenu qu’à l’instant t=0 on a : x=0 , la solution de cette équation est :

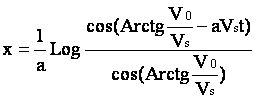
Cette relation peut aussi s’écrire plus simplement:

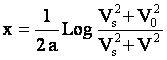équation [3]

La vitesse V s’annulera au bout d’un temps t_A donné par :

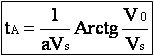
La distance x_A parcourue par le cycliste jusqu’à l’arrêt sera égale à :

Second cas : faible freinage B< W(p-f)

On posera alors :

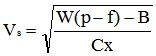
Avec cette notation, l’équation devient :

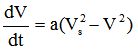
soit

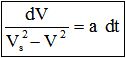
Sachant qu’au temps t=0 où le cycliste freine, la vitesse est égale à V0, l’intégration de cette équation, toujours en supposant que B reste constant dans le temps, conduit à la relation ci-après donnant le temps t nécessaire pour atteindre une vitesse V:

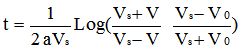équation [4]

De cette relation, on peut tirer la vitesse V, soit :

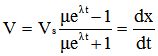équation [5]

après avoir posé :

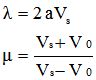
On constate donc que lorsque le temps augmente, la vitesse ne s’annule pas mais tend vers une vitesse limite égale à Vs. Le freinage est insuffisant pour s’arrêter, il sert uniquement pour rouler moins vite, ce qui concerne notamment la descente des cols.

L’intégration de cette équation conduit à la relation ci-après donnant la distance parcourue au bout d’un temps t

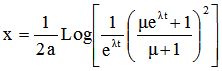équation [6]

En éliminant le temps entre les équations [5] et [6], on peut obtenir la relation entre la distance parcourue x et la vitesse V:

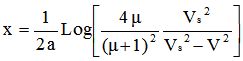équation [7]

La force de freinage

Quel peut être l’ordre de grandeur de la force de freinage B ?

Pour répondre à cette question, examinons comment s’obtient cette force B. Il faut prendre en compte :

les forces b1 et b2 exercées sur les manettes. Ces forces se transmettent aux patins de frein par un double système de leviers : celui des manettes et celui des étriers. Nous n’entrerons pas ici dans les technologies diverses des différents systèmes de freinage.
Aux manettes, l’effort est amplifié par le rapport x/y (voir figure 2). Ce rapport est de l’ordre de 3 à 5.
Aux étriers, le rapport peut être amplificateur, rarement réducteur bien que cela puisse exister.
L’effort ainsi transmis sur les patins va s’appliquer perpendiculairement aux jantes et va se transformer en effort tangentiel sur les jantes qui est fonction du coefficient de frottement entre la jante et le patin. Ce coefficient de frottement est de l’ordre de 0.5 Cela veut dire que si la force exercée par le patin est de 10 N, la force tangentielle sur la jante sera de 5 N.
Pour obtenir l’effort au niveau du contact entre le vélo et la route, il faut encore tenir compte du fait que le diamètre de la jante est un peu plus faible que le diamètre extérieur du pneu, ce qui conduit à une réduction de la force tangentielle dans le rapport D/J (D diamètre du rayon extérieur du pneu et J diamètre moyen de la jante).
les frottements : celui du câble dans sa gaine, celui des points de rotation. Ce frottement est important, il peut abaisser l’effort transmis de 50% voire plus.
l’existence de ressorts dans les étriers destinés à écarter les patins lorsque l’on relâche les manettes

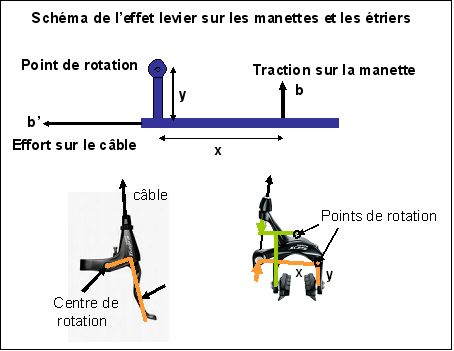
Fig.2. Schématisation de l’effet levier du système de freinage

Finalement, on peut exercer sur une roue une force B de freinage de l’ordre de 3 à 4 fois b. L’effort b qu’un cycliste exerce couramment sur une manette est évalué entre 30 et 60 N. En agissant sur les deux manettes, le cycliste peut donc produire une force de freinage totale pouvant aller jusqu’à 500 Newtons.
Notons que le risque de rupture du câble par excès de traction est nul. En effet la résistance d’un câble de frein, généralement constitué par un toron de 19 fils en acier de très forte résistance, est de l’ordre de 3000 Newtons, donc très largement supérieure à l’effort exercé par le cycliste. Si un câble se rompt, c’est par usure progressive de plusieurs fils ou par défaillance du sertissage des embouts.
En pratique, lors d’une randonnée, on n’exerce pas des forces très élevées lors des nombreuses opérations de freinage que l’on est amené à effectuer. Ce n’est seulement que dans des cas exceptionnels que la force devient importante. C’est pourquoi, nous distinguerons :

Le freinage usuel : c’est celui que l’on exerce lorsque l’on veut ralentir ou bien s’arrêter devant un obstacle aperçu de loin. Une force de freinage ne dépassant pas 150 N paraît suffisante pour répondre à cet objectif. Prenons par exemple, le cas d’un cycliste qui veut réduire sa vitesse dans une longue et forte descente. Pour calculer la force B, on prendra l’équation [1] et on écrira que l’accélération est nulle, d’où :
B=W(p-f)-CxV²

Ainsi, en prenant W=800 N f=0.01 Cx=0.20 il suffit d’exercer une force de freinage de 67 N pour réduire sa vitesse à 18 km/h dans une descente de 10%.
Le freinage d’urgence : c’est celui qui consiste à vouloir s’arrêter le plus rapidement possible, pour parer généralement un obstacle imprévu et soudain: piéton ou animal qui traverse, chute d’un cycliste qui précède, voiture qui coupe la route ou autres. Le freinage des coureurs cyclistes qui, à l’approche d’un virage dans la descente d’un col, cherchent à grappiller quelques secondes, peut aussi être assimilé à un freinage d’urgence. Dans un freinage d’urgence, on peut exercer des forces de 300 à 500 N, le problème qui se pose alors est d’éviter une chute par blocage d’une roue ou par culbute comme on le verra plus loin.

Le freinage constant

Comme indiqué précédemment, le freinage constant consiste à maintenir la même force sur les manettes durant toute l’opération de freinage. Faisons une application numérique. On adoptera les paramètres suivants

poids du cycliste avec son vélo 800 N
coefficient de pénétration dans l’air Cx=0.2
coefficient de frottement f=0.01
force de freinage B=250 N
vitesse initiale 36 km/h (10 m/s)
deux valeurs de pente ont été traitées : 0 et 6% (descente)

Les temps d’arrêt sont respectivement de 3.02 sec et 3.7 sec
Les distances d’arrêt sont de 14.9 m et de 18.2 m
La figure 3 présente les courbes donnant la vitesse et la distance parcourue en fonction du temps. Sur la figure 4, on trouvera la courbe donnant la variation de la vitesse en fonction de la distance.

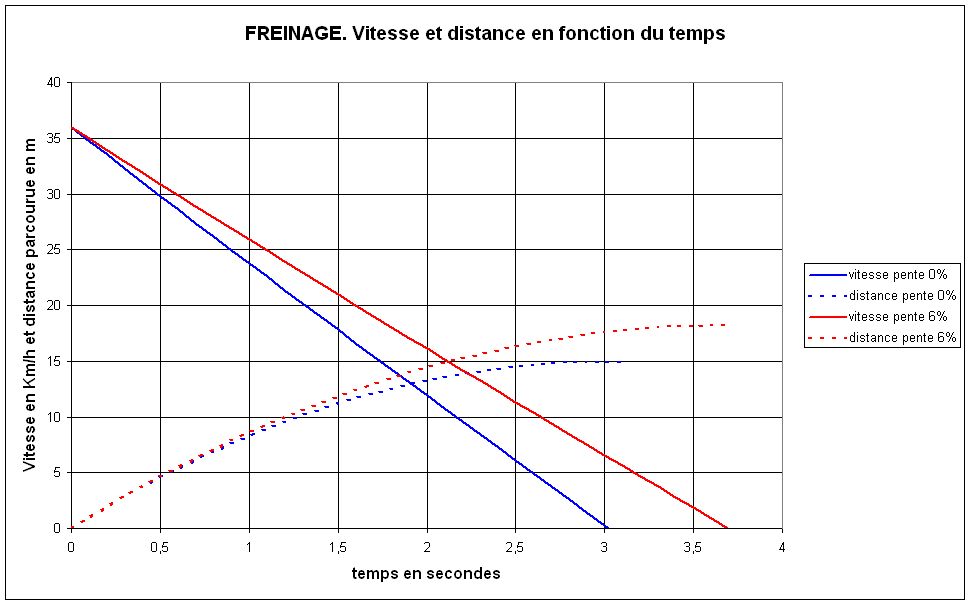
Fig.3. Diagrammes du freinage avec force de freinage constante

Le freinage progressif

En pratique, freiner en maintenant une force B à peu près constante se réalise souvent dans une descente avec pour objectif de garder une vitesse constante. En revanche, maintenir une force B constante lorsque l’on veut s’arrêter, par exemple lorsque l’on aperçoit un panneau STOP, est illusoire car il faudrait que le cerveau humain puisse instantanément adapter la valeur de cette force à la distance qui le sépare du panneau, ce qui paraît impossible. Le cycliste va donc réguler la force B au fur et à mesure qu’il s’approche du point d’arrêt souhaité. Il existe mille manières de faire cette régulation. On les classera cependant en deux types : le type progressif et le type dégressif.
Le type progressif consiste à augmenter progressivement la force B.
Examinons cette manière de freiner en supposant que le cycliste augmente la force B de façon linéaire dans le temps.
On peut écrire :

B=B0 + λt

λ est un paramètre positif définissant l’augmentation de la force B par seconde.

L’équation [1] n’ayant pas de solution analytique, il faut la résoudre numériquement. C’est ce qui a été fait en reprenant les caractéristiques de notre cycliste.

On a fixé la valeur de B0, force exercée lorsque le cycliste commence le freinage à 200 N et on a déterminé la valeur qu’il fallait donner à λ pour que le cycliste s’arrête après avoir parcouru la même distance que dans l’exemple de la figure 3 où la force de freinage reste constante et égale à 250 N, soit 14.9 m. On a obtenu λ= 49.5. La valeur de B est donc donnée par:

B=200 + 49.5 t

Sur la figure 4, on a tracé la courbe donnant la vitesse en fonction de la distance. On constate évidemment qu’au début du freinage, la vitesse diminue moins vite et qu’à la fin du freinage la vitesse diminue plus vite que dans le cas à B=constante. Le temps mis pour s’arrêter est plus court: 2.79 secondes.

Le freinage dégressif

Le type dégressif consiste à freiner très fort au début puis à relâcher progressivement les manettes de frein.

Pour illustrer par des calculs ce mode de freinage, on adoptera là encore l’hypothèse d’une variation linéaire de la force B dans le temps. Le coefficient λ est alors négatif.
Dans l’application numérique qui a été effectuée avec intégration numérique de l’équation [1], on a fixé à 300 N la valeur initiale de la force B et l’on a déterminé la valeur de λ pour que le cycliste s’arrête après avoir parcouru la même distance de 14.9 m. On a trouvé λ=-44.4. La valeur de B est donc donnée par :

B=300 – 44.4 t

La courbe montrant la diminution de la vitesse en fonction de la distance est tracée sur la figure 4.
On constante évidemment une plus forte décroissance de la vitesse au début du freinage et une plus faible décroissance à l’approche du point d’arrêt. Le temps de freinage est allongé par rapport aux autres modes de freinage: 3.8 secondes.

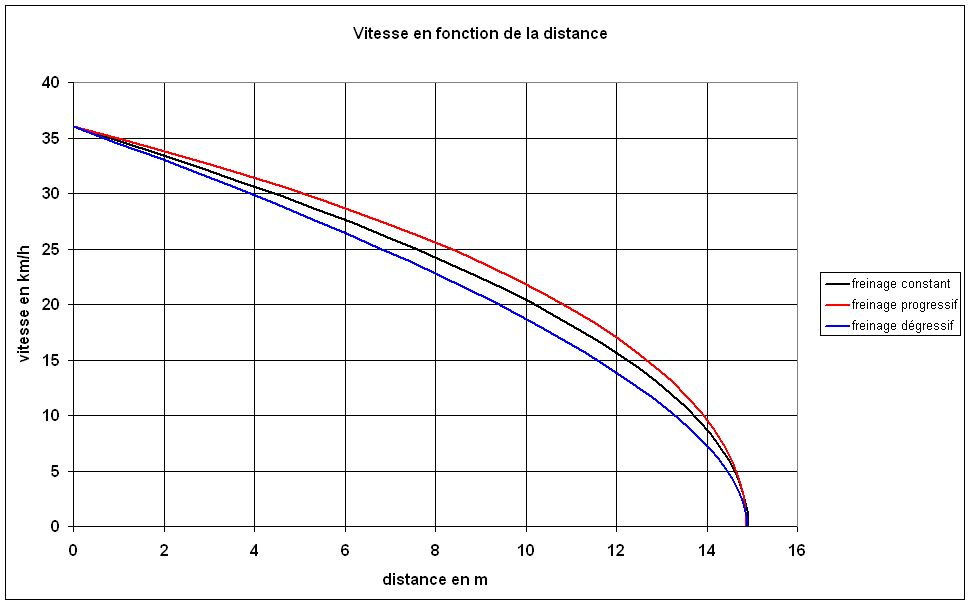
Fig.4. Comparaison de 3 manières de freiner

Energie dissipée lors du freinage

L’énergie mécanique que fournit le cycliste en appuyant sur les manettes se transforme en chaleur provoquée par le frottement entre les patins et les jantes. Il suffit de toucher les jantes après la descente d’un col pour s’en convaincre.
La valeur de cette énergie, c’est-à-dire de la force B, est donnée par l’intégrale :

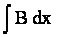
Dans le cas où B reste constant, l’énergie est donc égale à : B x_A x_A étant la distance d’arrêt.
Si B est variable, il faut connaître la variation de B en fonction de x, ce qui est le cas si l’on résout par méthode numérique l’équation [1].
Avec les applications numériques faites précédemment, on obtient :

pour B=constante= 250 N, l’énergie est de : 3726 Joules
pour B progressif avec B=200 + 49.5 t, l’énergie est de : 3680 Joules
pour B dégressif avec B= B=300 – 44.4 t, l’énergie est de : 3770 Joules

On constate, ce qui peut un peu surprendre, que l’énergie n’est pas la même dans les 3 cas. Dans le freinage progressif, cela s’explique par le fait, que le freinage étant plus doux au départ, donc la diminution de vitesse plus lente, on profite mieux de la résistance de l’air qui a un rôle de frein, rôle que chacun peut constater en se redressant sur son vélo dans une descente. Pour le freinage dégressif, c’est l’inverse, on perd un peu de l’effet de frein de l’air. On en arrive donc à la conclusion que le freinage dégressif use plus les patins de frein que le freinage progressif, ce qui n’est vraiment pas d’une importance primordiale.

Risque de culbute

Le risque de culbute vers l’avant est appréhendé par beaucoup de cyclistes, notamment dans les descentes où l’on a le sentiment qu’un coup de frein sur la roue avant va nous faire passer par dessus le guidon. En pratique, les chutes obtenues par basculement sont plus rares que les chutes dues au glissement que l’on étudiera plus loin, c’est surtout lorsque l’on heurte un obstacle que le risque de culbute est notable.
Lors d’un basculement, il est évident que le premier évènement qui se produit est un décollement du sol de la roue arrière. Quelles sont donc les conditions à remplir pour obtenir ce décollement ?

Le décollement de la roue arrière

Lors d’un freinage, la force d’inertie modifie la répartition du poids sur les roues : la roue avant va être surchargée et la roue arrière déchargée. Il nous faut donc évaluer cette nouvelle répartition du poids ainsi que la force d’inertie.

Condition du décollement.

La figure 5 représente les forces en présence : la force de gravité W et la force d'inertie Fi

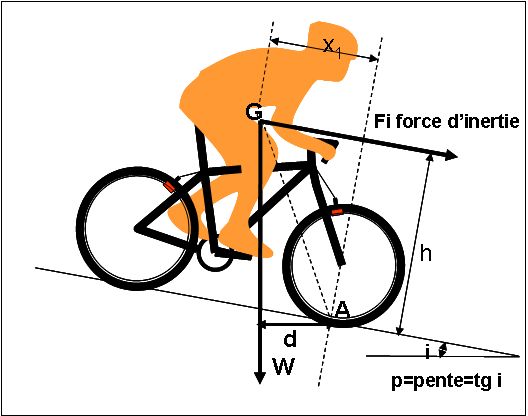
Fig.5. Condition du décollement de la roue arrière : rotation autour du point A

Lors d'un fort coup de frein, la roue arrière décollera si l'on a :

h Fi > d W

équation [8]

d est la distance entre le point A et la verticale du centre de gravité. Cette condition exige que cette verticale se situe en amont du point A, sinon le cycliste basculera même à l'arrêt.
Il faut donc connaître la position du centre de gravité ainsi que la valeur de la force d'inertie.

Position du centre de gravité G de l'ensemble vélo-cycliste.

On notera (voir figure 7) :

h la hauteur du centre de gravité G
x₁ la distance entre G et la verticale de l’axe de la roue avant
x₂ la distance entre G et la verticale de l’axe de la roue arrière
E la somme x₁+x₂, c’est-à-dire l’entraxe entre les deux roues

Les valeurs de x1 et x2 sont faciles à déterminer : il suffit de disposer d'un pèse-personne. On pèse d'abord l'ensemble vélo et cycliste, on obtient le poids W. Ensuite, on place le pèse-personne sous la roue avant et le cycliste se met en position. On obtient le poids W1.
Si E est l'entraxe entre les deux roues, distance facile à mesurer (l'entraxe pour un vélo de route est compris entre 95 cm et 105 cm), les valeurs de x1 et x2 sont données par :

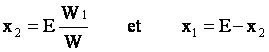
Pratiquement, pour un vélo de route, le centre de gravité se situe à la hauteur de la selle, un peu en avant du bec de selle. Evidemment, cette position varie un peu avec la position du cycliste sur son vélo ainsi qu'avec le mouvement des jambes.
La distance d s'écrit donc :

d=x₁ cos i - h sin i

Cette valeur doit être positive, afin que la verticale du centre de gravité se situe vers l'amont. On doit donc avoir la condition:

tg i < d/h

Valeur de la force d'inertie Fi.

Par définition de la force d'inertie, Fi est une force fictive qui équilibre la force d'accélération dans l'équation du mouvement du cycliste. On a donc :

On a donc :

Fi=W(f-p)+Cx V²+B

La force Fi doit être positive, c'est-à-dire dirigée dans le sens du mouvement, ce qui revient à dire que le cycliste doit être en décélération. En conséquence, la condition suivante doit être respectée si l'on veut un décollement :

B > W(p-f)-Cx V²

En reprenant l'équation [8], la force de freinage Bc nécessaire pour obtenir le décollement est finalement :

équation [9]

Reprenons notre cycliste standard pour une application numérique. La figure 5 donne la force Bc nécessaire pour décoller la roue arrière en fonction de la vitesse du cycliste.

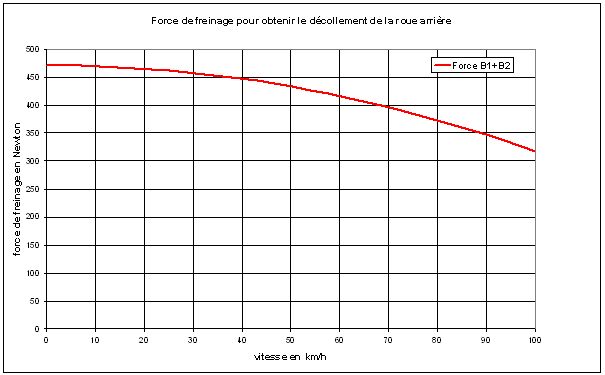
Fig.6. Force de freinage pour décoller la roue arrière.

On peut remarquer :

que cette force reste relativement constante dans la plage 0-40 km/h lorsque la vitesse du cycliste varie.
pour des vitesses très élevées, cette force diminue : il faut donc moins « freiner » si l’on va très vite afin d’éviter une chute.
que la valeur de cette force est cependant importante, il faut donc serrer très fort les manettes de freins si l’on désire culbuter, ce qui n’est quand même pas l’objectif du cycliste.
que l’on peut décoller la roue arrière même à vitesse très faible. On peut constater facilement ce phénomène lorsque, en marchant à pied et en poussant son vélo, on serre brutalement le frein avant : la roue arrière décolle.

Que se passe t-il après le décollement de la roue arrière ?

La relation [9] donnant la force de freinage Bc déclenchant le décollement de la roue arrière ne fait pas de distinction entre roue avant et roue arrière. Cette force de freinage est la force totale de freinage. Peu importe qu’elle soit exercée sur l’un ou l’autre des freins ou sur les deux freins en même temps. En revanche, c’est après le décollement que cela change.
Si le freinage est exercé uniquement sur la roue arrière, dès le décollement, la force de freinage tombe à zéro puisque la roue ne touche plus le sol. La roue va alors retomber et retoucher le sol, puis redécoller et ainsi de suite. Ce n’est donc pas à proprement parler une culbute qui s’ensuivra mais plutôt un glissement. Une chute est alors fort probable.
Si le freinage est exercée uniquement sur la roue avant, la culbute est inévitable sauf si, en une fraction de seconde, le cycliste relâche le frein. Dans ce dernier cas, le cycliste aura raté son freinage puisqu’il aura toutes chances de percuter l’obstacle objet du freinage. Nous ne mettrons pas en équation le mouvement de rotation du vélo et du cycliste, l’intérêt de connaître la vitesse à laquelle la tête du cycliste heurtera le sol étant restreint. L’objectif est de ne pas se mettre en condition de culbute.

Le risque de dérapage

Un second risque du freinage est le dérapage : en exerçant une force de freinage trop grande sur une roue, on peut la bloquer, le pneu glissera sur la chaussée, ce qui entraînera une perte de contrôle de la direction.
Le mécanisme de dérapage est un problème de frottement. Il faut bien savoir en effet que c’est grâce au frottement entre le pneu et la chaussée qu’un cycliste peut rouler. On se rend compte aisément de cela si l’on veut rouler sur un sol verglacé : la moindre accélération risque de vous faire patiner et le moindre freinage risque de vous faire glisser. Sans l’existence de frottement pneu-chaussée, on ne pourrait pas rouler.

Comme un glissement peut affecter seulement l’une des deux roues, il est nécessaire de distinguer maintenant la roue avant et la roue arrière.

Formulation du problème

Pour bien comprendre le mécanisme d’adhérence d’un pneu à la chaussée, imaginons l’expérience suivante :

vous fixez votre vélo sur un support pour rendre libre une roue
vous prenez une planchette (qui simule la chaussée) et vous l’appliquer sur la roue pour la faire tourner (figure 6). La roue tournera dès que vous effleurez le pneu si aucune résistance ne s’oppose à la rotation de la roue
appuyez maintenant sur la manette de frein. Les patins exercent alors sur la jante une force B. Ce sera plus difficile de faire tourner la roue, un simple effleurement ne suffit pas, il faut appuyer fortement la planchette contre le pneu pour la faire tourner et cela sera même difficile si la planchette est très lisse, un peu moins si la planchette est rugueuse. Autrement dit, non seulement, il faut exercer une force T tangentielle à la roue mais il faut aussi exercer une force N perpendiculaire à la roue. La force T que vous voulez exercez sur la roue par l’intermédiaire de la planchette se transmet à la roue grâce au frottement entre la planchette et le pneu. Pour que la roue puisse tourner, il faut que deux conditions soient satisfaites :

la force T doit être supérieure à la force B induite par les patins de frein donc T>B
la force N doit être telle que l’on ait :

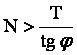
φ est l’angle de frottement et tgφ est le coefficient de frottement
Cette relation s’écrit aussi : T < N tg φ

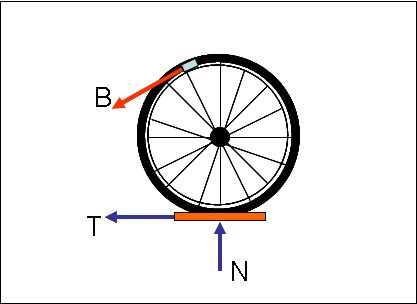
Fig.7. Transmission d’un effort sur la roue par frottement

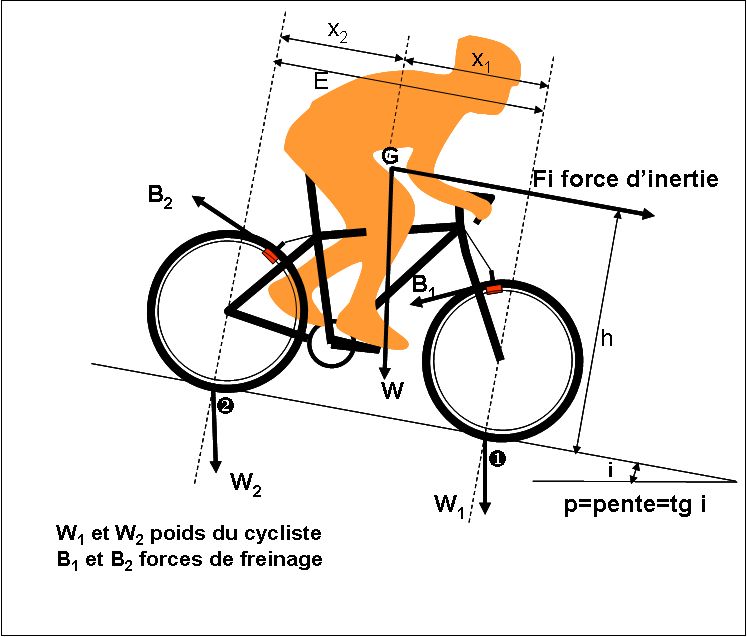
Fig.8. Forces à prendre en compte lors d’un dérapage

Transposons cette condition au cycliste en train de freiner (voir figure 7).

W₁ et W₂ sont les réactions du sol sur les roues avant et arrière. Elles équilibrent le poids W du cycliste et de son vélo. Sur une route pentée, ces forces ne sont pas perpendiculaires à la chaussée, on peut les décomposer en force perpendiculaire et en force tangentielle. Ce sont les composantes perpendiculaires W₁ cos i et W₂ cos i qui nous intéressent.
B₁ et B₂ sont les réactions aux forces de freinage qu’il faut vaincre si l’on veut que la roue tourne

Pour la roue avant :

la force N perpendiculaire à la chaussée est due à la fraction du poids du cycliste exercée sur la chaussée. Elle est égale à : W₁ cos i
la force tangentielle T qu’il faut appliquer à la roue, au contact pneu-chaussée, pour la faire tourner doit être supérieure à B₁

La condition de non glissement s’écrit donc:

B₁ < W₁ cos i tg φ

Pour la roue arrière, la condition s’écrit:

B₂ < W₂ cos i tg φ

Les valeurs de W₁ et W₂ ont été calculées précédemment ainsi que la force d’inertie

Les conditions de non glissement s’écrivent donc :

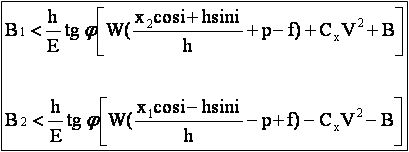
ou encore :

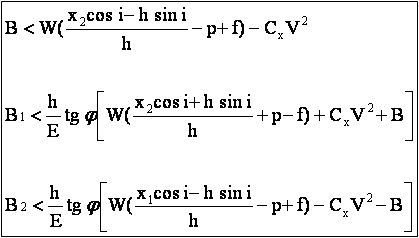
Si l’on ne veut pas faire la distinction entre roue avant et roue arrière, la force de freinage totale Bg=B₁+B₂ qu’il ne faut pas dépasser est égale à :

Bg=W cos i tg φ

Cette relation est purement mathématique, elle signifie seulement que si l'on exerce un effort de freinage égal ou supérieur à Bg, on peut être sûr de déraper. En adoptant un angle de frottement de 40 degré , valeur qui nous paraît être standard sur une route normale (voir paragraphue suivant) et, l'angle i étant relativement faible, en arrondissant cos i à 1, cela veut donc dire que l'effort de freinage ne doit pas dépasser 0.8 W, c'est-à-dire qu'il ne faut pas exercer un effort de freinage supérieur à 80% de son poids.
Il faut noter que ne pas faire de distinction entre roue avant et roue arrière, n'a guère de signification physique, si ce n'est que l'on transforme un vélo en un solide glissant ou roulant sur un plan et donc que l'on supprime la propriété essentielle d'un deux roues lors d'un freinage qui est d'accroître l'effort vertical sur la roue avant et de soulager la roue arrière.

Valeur du coefficient de frottement φ

Tout d’abord, il ne faut pas confondre ce coefficient de frottement avec le coefficient f figurant dans l’équation [1] du mouvement du cycliste, Le coefficient f que l'on appelle également "coefficient de résistance au roulement" caractérise le contact avec la chaussée d’une roue qui tourne alors que tgφ caractérise le frottement d’une roue bloquée.
Ce coefficient tgφ varie en fonction de l’état de la route : la texture de la route et son humidité. Pour une route sèche normalement goudronnée, ce coefficient serait voisin de 0.8 (angle φ de l’ordre de 40 degré) et proche de 0.4 pour une route mouillée.
Une route forestière humide tapissée de feuilles mortes en automne offre un bien plus faible coefficient. Cela devient pire si la route est verglacée.

Ce coefficient tgφ varie aussi en fonction de l’état des pneus. Cela est de votre responsabilité. Non seulement un pneu de vélo ne dispose pas de repère d’usure mais aussi aucune verbalisation par la force publique n’est à craindre pour des pneus trop usés.

Application numérique. Cas 1 : freinage constant

Reprenons notre cycliste standard et cherchons à calculer les forces de freinage B₁ et B₂ qu’il ne doit pas dépasser. Nous prendrons :

h=1 m
x₁=0.60 m
x₂=0.40 m donc E=1.00 m
φ=40 degré soit tg φ= 0.84

Il faut ensuite connaître la variation de vitesse V en fonction du temps.
Comme on l’a vu, l’équation du mouvement [1] n’a une solution analytique que dans le cas où B=B₁+B₂ est constant.
En prenant B=B₁+B₂ égal à 250 N, la figure 9 donne les valeurs de B₁ et B₂ qu’il ne faut pas dépasser tout au long de l’opération de freinage.

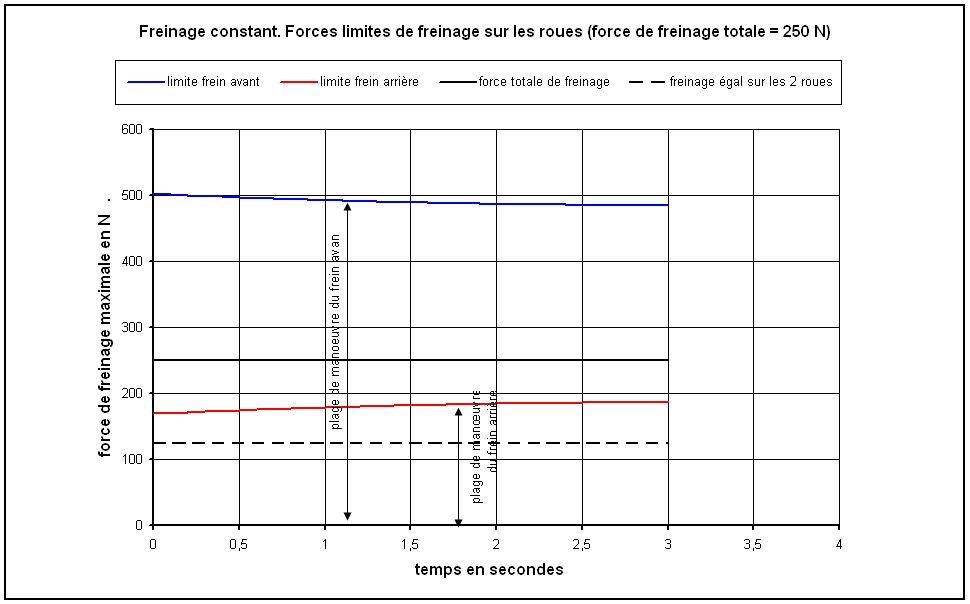
Fig.9. Freinage constant de 250 N. Forces limites sur les roues avant et arrière

On constate que la force limite admissible sur la roue avant est forte, voisine de 500 N ce qui veut dire qu’en freinant avec 250 N sur la roue avant, il est impossible de déraper.
En revanche, si l’on freine uniquement avec la roue arrière, le dérapage est assuré.
Si le cycliste répartit la force de freinage totale de 250 N de façon égale sur les deux roues, donc 125 N par roue, aucune roue ne glissera.

Application numérique. Cas 2 : freinage progressif

Reprenons les mêmes valeurs que précédemment pour définir un freinage progressif défini par la relation:

B=200 + 49.5 t

Sur la figure 10 on a tracé les courbes correspondant à ce freinage donnant les valeurs de la force de freinage à ne pas dépasser pour éviter un glissement.
Là encore on constate qu’il n’y a aucun problème pour freiner fortement sur la roue avant, le dérapage est impossible.
En revanche, en freinant uniquement avec le frein arrière, le dérapage de la roue arrière est là encore immédiat.
Si le cycliste met la même force sur le frein avant et le frein arrière, soit au départ 100 N sur chaque roue. On a tracé sur la figure 10 la force de freinage sur chaque roue en fonction du temps, soit au départ 100 N sur chaque roue : on constate sur le graphique qu’après un laps de temps d’environ 2 secondes, la force B2 aura dépassé la limite autorisée. Il y aura alors dérapage de la roue arrière. Si cela se produit, il faut que le cycliste relâche immédiatement le frein arrière s’il arrive à se rétablir.

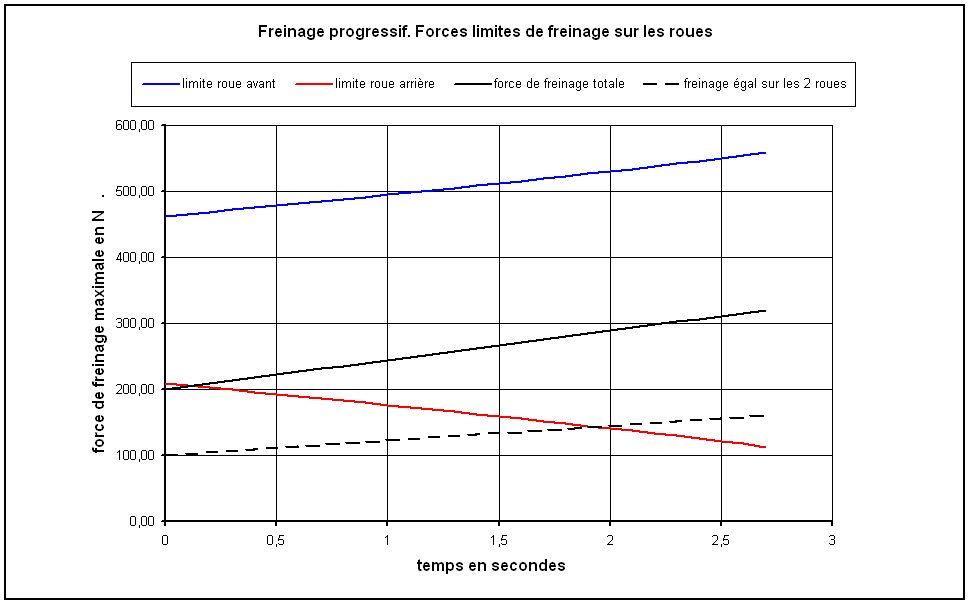
Fig. 10. Freinage progressif. Forces limites sur les roues avant et arrière

Application numérique. Cas 3 : freinage dégressif

Sur la figure 11 on a tracé les mêmes courbes que précédemment correspondant à un freinage dégressif défini par :

B=300 – 44.5 t

Là encore on constate qu’il n’y a aucun problème pour freiner uniquement sur la roue avant tandis que c’est le dérapage immédiat en freinant sur la roue arrière.
Si le cycliste utilise les deux freins à part égale soit 150 N au départ du freinage, un dérapage de la roue arrière se produira. On freinera donc d’abord sur la roue avant et ce n’est que plus tard que l’on pourra utiliser le frein arrière.

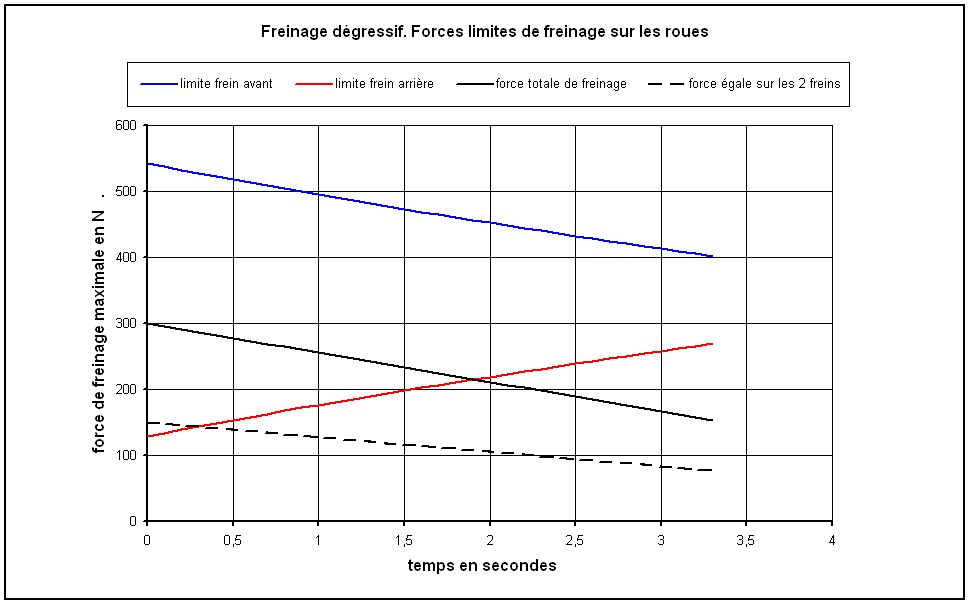
Fig.11. Freinage dégressif

Synthèse : comment gérer correctement son freinage

L’équation générale [1] a été établie sans prendre en compte la limitation de la force de freinage B. On vient de voir que non seulement la valeur totale de cette force doit être limitée mais aussi que la répartition de cette force sur les deux roues doit être prise en compte afin d’éviter un dérapage ou une culbute.
Les trois conditions à remplir pour éviter une chute sont reprises ci-dessous:

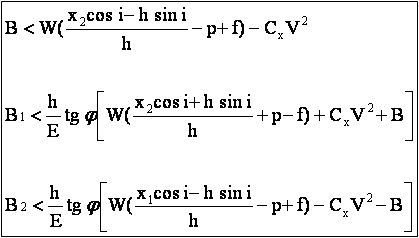
Ces relations attirent les remarques suivantes :

les forces limites de glissement sont proportionnelles au coefficient de frottement tg φ qui peut varier dans des proportions assez grandes, facilement du simple au triple alors que la force limite de culbute reste relativement constante. L’état de la chaussée est donc primordial.
les forces limites de glissement sont elles mêmes fonctions de la force totale de freinage. Plus on freine fort, plus la force limite de freinage sur la roue avant est forte et plus la force limite sur la roue arrière est faible. Le risque de glissement sur la roue arrière est le risque prépondérant.

Appliquons ces conditions à notre cycliste standard et faisons le rouler à 36 km/h sur trois chaussées : une chaussée normale (tgφ=0.84), une chaussée glissante (tgφ=0.40), et une chaussée extrêmement glissante (tgφ=0.20), ce qui peut arriver par exemple en présence d’une tache d’huile. Les tableaux ci-dessous donnent les conséquences du freinage en fonction de l’intensité du freinage et de sa répartition sur les roues avant et arrière.

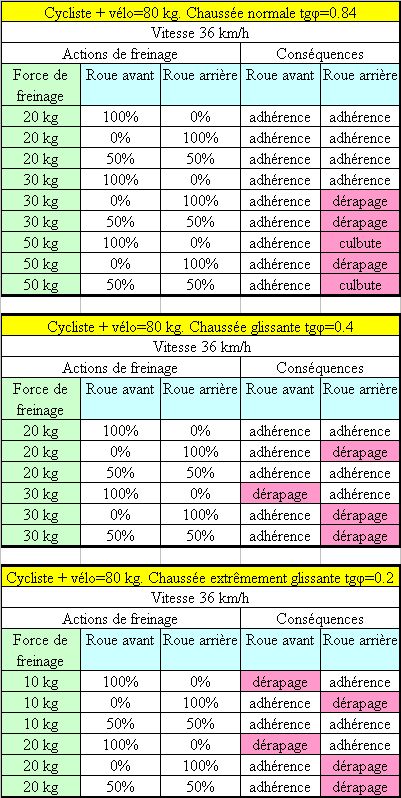
On en tire les conclusions suivantes :

en exerçant une force de freinage inférieure à 100 N soit 10 kg, le risque de chute est pratiquement nul. Cette force s’obtient en exerçant une traction sur chaque manette de frein de l’ordre de 1 à 2 kg, ce qui est tout à fait modéré. Avec cette force, la distance d’arrêt sera de 11 m si l’on roule à 20 km/h, de 24 m à 30 km/h, de 41 m à 40 km/h, ce qui permet de parer tout obstacle aperçu à l’avance. Comme on l’a vu, cette force est aussi suffisante pour descendre une pente à 10 % à une vitesse très faible.
le risque le plus fréquent est celui du dérapage de la roue arrière. Pour éviter cela, il vaut mieux exercer la force de freinage de façon privilégiée sur le frein avant.
le risque de culbute ne devient notable que pour une force de freinage importante, c’est-à-dire lors d’un freinage d’urgence.

Le freinage d’urgence

Sachant que le freinage d’urgence présente des risques, la question importante est de savoir sur quelle distance on peut espérer pouvoir s’arrêter sans risquer de culbuter ou de déraper. Reprenons nos applications numériques. Avec un coefficient de frottement de 0.8 donc une chaussée normale, le risque de glissement s’obtient pour Bg = 640 N sur une route plate. Quant au risque de culbute, il est fonction de la vitesse initiale, la figure 11 montre que la force Bc est comprise entre 400 et 500 N. On dira donc que sur une chaussée « normale », c’est le risque de culbute que l’on peut craindre en premier, à condition, bien sûr, que le freinage ne se fasse pas sur la roue arrière.
La force de freinage maximale pour éviter tout incident est donc la force Bc. Pour s’arrêter le plus rapidement possible, le cycliste exercera sur la roue avant une force à la limite de la culbute. Cette force limite est donc donnée par l’équation [9].
On va supposer que le cycliste serre le frein très fort en maintenant la même force durant l’opération de freinage c’est-à-dire durant quelques secondes, ce qui est une hypothèse tout à fait réaliste.
En combinant les équations [3] et [9] , on obtient la relation suivante donnant la distance minimum d’arrêt :

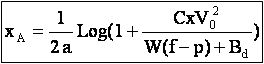
Appliquons cette relation à notre cycliste standard. La figure donne la distance d’arrêt en fonction de la vitesse initiale.
On peut constater qu’un cycliste roulant à moins de 20 km/h peut s’arrêter en moins de 3 m. Un professionnel roulant au voisinage de 45 km/h ne pourra s’arrêter qu’au bout d’une quinzaine de mètres. Dans le cas d’une chute dans un peloton, il est donc improbable que les coureurs se trouvant à moins de quinze mètres de cette chute, puissent éviter de chuter à leur tour. Dans une forte descente où un coureur atteint 90 km/h, une distance de 75 m est nécessaire pour s’arrêter.

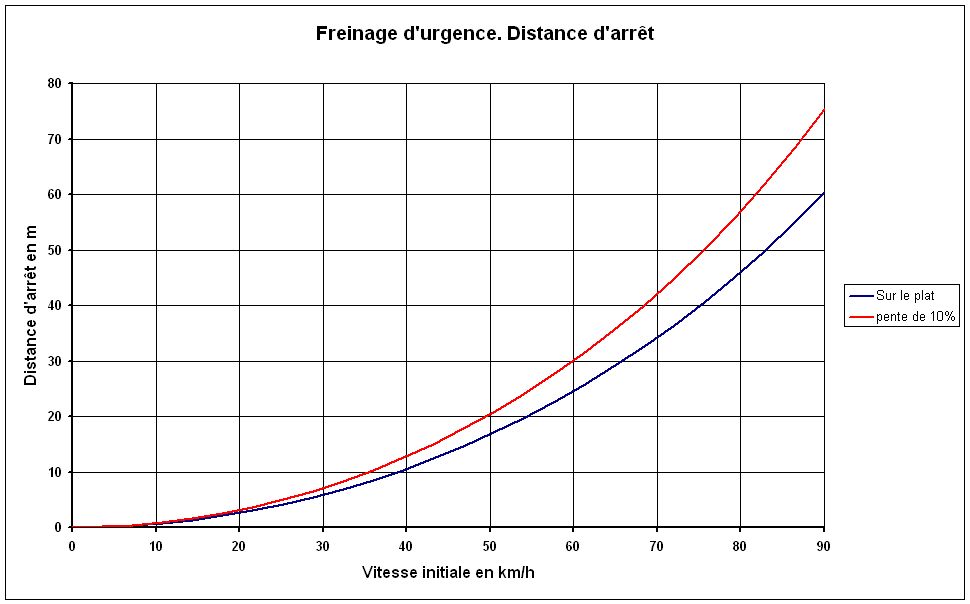
Fig.12. Distance minimum d’arrêt

Conclusions pratiques

L’approche mathématique du freinage effectuée dans ce document confirme des règles connues et permet de les quantifier. On les résumera ainsi :

la force que le cycliste exerce sur les manettes est de l’ordre de 1 à 2 kg par manette lors d’un freinage doux
la force que les patins de frein exercent sur les jantes est de l’ordre de 10 à 20 kg pour un freinage doux. Elle peut atteindre 40 à 50 kg pour un freinage d’urgence
il ne faut pas exercer la même force sur les deux manettes mais privilégier le frein avant afin d’éviter un dérapage sur la roue arrière
avec un freinage progressif, on risque plus facilement un dérapage de la roue arrière en fin de freinage
un freinage dégressif est le plus sûr, à condition, bien sûr, qu’il ne soit pas excessif au départ
un freinage excessif sur la roue avant peut provoquer une culbute, un ordre de grandeur de l’effort de freinage sur les jantes initiant la culbute est de 40 à 50 kg.
il ne faut guère utiliser le frein arrière lors d’un freinage d’urgence
un bon ordre de grandeur de la distance d’arrêt qu’il est possible d’obtenir lors d’un freinage d’urgence s’obtient en élevant au carré la vitesse en km/h et en divisant le résultat par 100. Exemple : à 40 km/h, on peut s’arrêter au bout de 40 x 40 = 1600/100=16 m.

Finalement, le freinage usuel est une opération sans risques. C’est le freinage d’urgence qui peut poser problème. En une fraction de seconde, le cycliste devra se rendre compte de l’état de la chaussée, de sa vitesse et ajuster l’effort de freinage en conséquence, ce qui demande une certaine expérience. Même des professionnels commettent des erreurs.
En août 2015, aux Etats-Unis, lors du Tour de l’Utah, un coureur irlandais a fait une chute assez effrayante, se soldant par de multiples fractures. L’origine de la chute est un freinage excessif réalisé avant de négocier un virage. Les deux vues ci-après, extraites de la vidéo que l’on peut voir sur Internet, semble montrer que la roue arrière a d’abord dérapé et ensuite qu’elle s’est décollé du sol : à ce moment là, le vélo n’était plus maitrisable et le coureur a percuté un véhicule suiveur. Par ailleurs, on peut se poser la question du choix de la trajectoire pour prendre le virage, l’option prise étant la plus mauvaise (Voir le document « A quelle vitesse aborder un virage ? »). Peut-être le coureur était-il gêné par des véhicules pour aborder le virage à l’extérieur comme les coureurs qui le précédaient.

Février 2016. Revu en 2019
contact@velomath.fr

RETOUR ACCUEIL