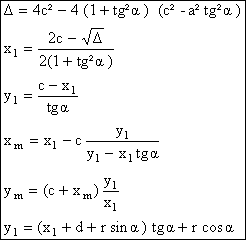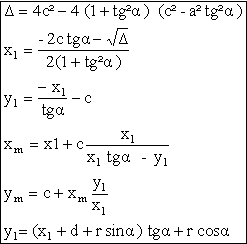ETUDE THEORIQUE DES PLATEAUX OVALES
 |
Avec un plateau ovale, |
Jacques Fine
Octobre 2012. Revu en Avril 2015
http://www.velomath.fr
contact@velomath.fr
Peu de temps après la course cycliste Paris-Nice en 2012, je suis tombé sur une publicité vantant les mérites des plateaux ovales car le vainqueur de cette course, Wiggins dont j’ignorais le nom avant sa victoire dans le Tour de France 2012, était équipé de ce matériel. Si l’on croyait aux dires de cette publicité: puissance accrue, pédalage plus souple, on pourrait se demander pourquoi tous les vélos de France ou d’ailleurs n’en sont pas équipés depuis longtemps puisque cette invention n’est pas nouvelle et date de plus d’une cinquantaine d’années, peut-être plus.
J’ai voulu en savoir davantage et notamment connaître la justification des avantages offerts par ce matériel. Je suis donc allé naviguer sur Internet. J’y ai trouvé beaucoup d’échanges sur des forums entre utilisateurs de ce type de plateau avec des avis contradictoires, certains louent les mérites de ce matériel, d’autres crient à l’arnaque. Certains estiment que l’on tourne plus « rond », ce qui à priori, peut être surprenant. J’ai aussi trouvé bien sûr des publicités sur ce matériel qui a pour nom: Bio-Space, Bio-Concept Stronglight, Rotor Q-Rings, O’Symetric, Ogival. En revanche, si j’ai pu aussi trouver des résultats de tests fort intéressants, je n’ai rien trouvé de bien clair sur la théorie et les calculs. J’ai donc tenté une formulation mathématique du problème en examinant d’abord comment un plateau ovale modifie la transmission de l’effort sur les pédales à la roue arrière.
Le mouvement de pédalage
Le cycliste exerce sur la pédale un effort P (voir figure 1). Cet effort peut se décomposer en deux :
- la composante radiale R dirigée suivant la direction de la manivelle. Cette force ne sert à rien. Un bon pédalage doit être telle que cette force soit très faible, sinon nulle
- la composante tangentielle F perpendiculaire à la manivelle : c’est cette force qui est motrice et va faire tourner les plateaux.
Nous ne retiendrons que la composante F. Notons bien que cette force varie lorsque la manivelle fait un tour, elle est la plus faible lorsque la manivelle se trouve dans les deux positions pseudo-verticales que l’on appelle les « points morts ». Pour simplifier les calculs, on admettra que les points morts correspondent à θ=0 et à θ=180°.
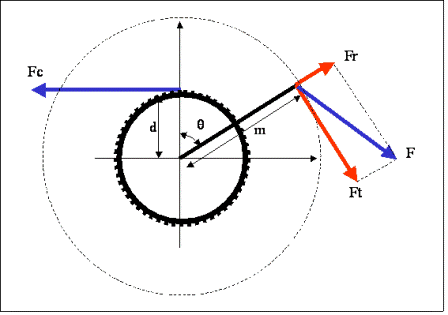
Fig.1. Composantes de l’effort exercé sur la pédale
Le couple moteur
La force F crée sur le pédalier un couple qui est égal à mF m est la longueur de la manivelle (valeur standard 17 cm). Dans le système d’unité international :
- >
- les forces s’expriment en newton et les longueurs en mètre.
- un couple s’exprime en newton-mètre soit N-m
Par l’intermédiaire de la chaîne, ce couple va être transmis au pignon arrière. Si l’on désigne
- par T la tension de la chaîne
- par p le rayon du pignon
la valeur du couple moteur s’exerçant sur le pignon arrière sera égal à pT.
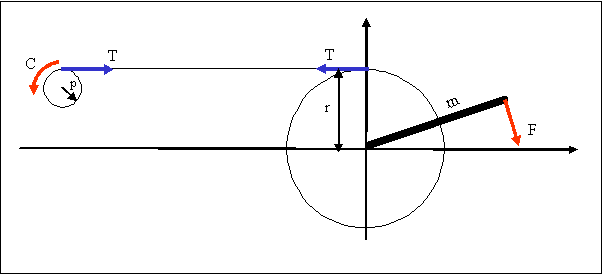
Fig.2. Equilibre des couples
Le couple résistant
Pour faire avancer un vélo, il faut vaincre des forces de résistance qui sont dues :
- à la résistance de l’air
- à la force de pesanteur
- au frottement pneus-chaussée
Ces forces sont explicitées dans notre document « Le vélo en équation » (référence [3]).
On peut les ramener à l’existence d’un couple résistant C s’exerçant sur le pignon de la roue arrière.
En écrivant l’égalité à chaque instant des couples moteur et résistant au pignon et au pédalier, on a donc:
C=pT et rT=mF
r est la distance entre la chaîne et l’axe du pédalier
On en déduit que la valeur du couple résistant C est relié au couple au pédalier mF par la relation :
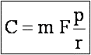
En réalité, la force motrice F est variable car le cycliste n’exerce pas la même force lorsque la manivelle est aux points morts ou en position horizontale alors que le couple résistant C est constant. Or, dans la relation [1], il y a égalité entre une fonction variable et une valeur fixe, ce qui est impossible. En fait, le couple moteur est tantôt supérieur au couple résistant et tantôt inférieur. Les principes de la dynamique nous disent que dans le premier cas, il y a accélération et dans le second cas décélération. Dans la réalité, la force d’inertie du vélo et du cycliste fera qu’il n’y aura pas d’à-coups.
Travail des couples
Lorsque le plateau fait un tour, le travail W de la force F doit être égal au travail du couple résistant. Ce travail doit donc s’écrire au moyen d’une intégrale, d'où la relation [1]:
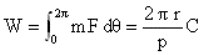
Le rapport r/p est le développement, on le désignera par d. Lorsque le plateau fait un tour, le pignon fait d tours.
Pour simplifier, nous admettrons que l’on a affaire à un cycliste idéal dont le travail des deux jambes est identique, on évaluera donc le travail seulement sur un demi-tour du plateau. Le travail de la force F lorsque la manivelle passe de la position verticale haute à la position verticale basse s’écrit donc par la relation [2] :<:p>

Comment évaluer la force F ? le test-ergocycle
La force F (ou le couple mF) est une donnée personnelle de chaque cycliste. Pour la connaître, il faut la mesurer en instrumentant le vélo. Pour cela, il faut équiper le vélo d’un capteur dit « capteur de puissance ». Il en existe de plusieurs types. Parmi ceux-ci, on peut retenir :
- le capteur type SRM qui se place dans le pédalier lui-même et qui mesure le couple transmis entre la manivelle et le plateau
- le capteur type Powertap qui s’intègre dans le moyeu de la roue arrière
Dans le cas qui nous intéresse, c’est le capteur SRM qui paraît le plus approprié puisqu’il mesure directement l’effort sur les manivelles.
Pour faire des tests reproductibles, il vaut mieux faire des essais en salle plutôt que sur route. Le test dit « ergocycle » va donc consister à placer un vélo sur un home-trainer, la roue arrière reposant sur un tambour associé à un frein. Le frein sera réglé à une valeur fixée et maintenue constante pendant le test. On enregistrera donc la valeur du couple et on tracera la courbe donnant la valeur du couple en fonction de l’angle de rotation de la manivelle.
Les figures 3 donnent les résultats de tests effectués avec un plateau circulaire. Ces résultats sont extraits d’études réalisées à la Section Sport de l’Université de Franche-Comté à Besançon dont on trouvera les références en fin de document.
L’examen de ces courbes attire les commentaires suivants :
- la courbe passe bien sûr par un minimum aux points morts c’est-à-dire lorsque les manivelles sont sub-verticales et par un maximum lorsque les manivelles sont sub-horizontales.
- les « arrondis » des courbes aux minimums et aux maximums ne sont pas identiques.
- il y a dissymétrie assez forte des deux jambes pour le graphique 3b: le corps humain est loin de fonctionner comme une machine
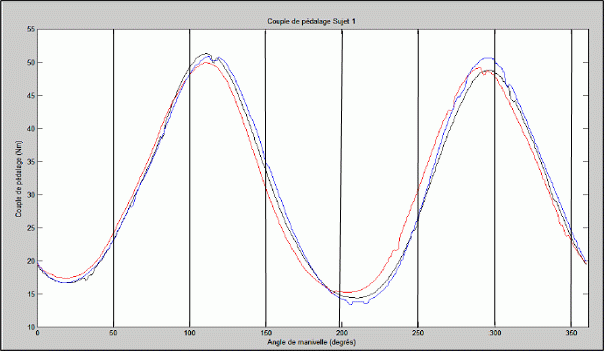
Fig.3a. Mesure du couple au pédalier avec un plateau circulaire
(3 courbes en fonction de la position de la selle) (tiré de bibliographie [1])
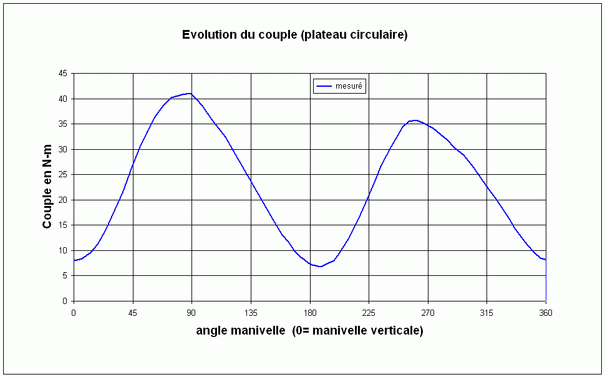
Fig.3b. Exemple de graphique de pédalage (tiré de bibliographie [2])
En conclusion, l’allure des courbes est variable en fonction de plusieurs paramètres et en priorité en fonction du sujet.
Modélisation du pédalage
Pour pouvoir effectuer des calculs, nous allons essayer de donner une formulation analytique au graphique de pédalage. Le problème est donc d’ajuster au mieux possible une fonction aux courbes expérimentales.
Pour simplifier cette fonction, nous supposerons que les minimums sont obtenus pour θ=0° et θ=180° et le maximum pour θ=90°
On admettra aussi que lors de la remontée de la pédale, la force F est nulle.
Nous proposons la relation [3] suivante pour estimer la force F lorsque l’angle θ varie de 0 à 180°
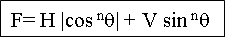
En prenant n=3, cette fonction s’ajuste bien à la courbe expérimentale de la figure 3a comme le montre la figure 4a. En revanche, il vaut mieux prendre n=2 pour le graphique de la figure 3b comme le montre la figure 4b.
Les paramètres H, V et n caractérisent donc le graphique de pédalage. Ce sont des paramètres propres à chaque cycliste.
On peut faire les commentaires suivants :
- A priori, cette formulation n’a pas de sens physique, c’est seulement un ajustement mathématique. Néanmoins, le paramètre H représente la valeur de la force lorsque la manivelle est aux points morts et le paramètre V représente la valeur de la force lorsque la manivelle est horizontale. On peut considérer alors que la force F provient de deux composantes :
- une force horizontale de valeur H cosn-1θ qui est maximale aux points morts pour s’annuler lorsque la manivelle est horizontale
- une force verticale de valeur V sinn-1θ qui est nulle aux points morts et prend son maximum pour θ=90°
- Lorsque l’exposant augmente de 2 à 3, cela induit un arrondi plus important pour les valeurs aux points morts
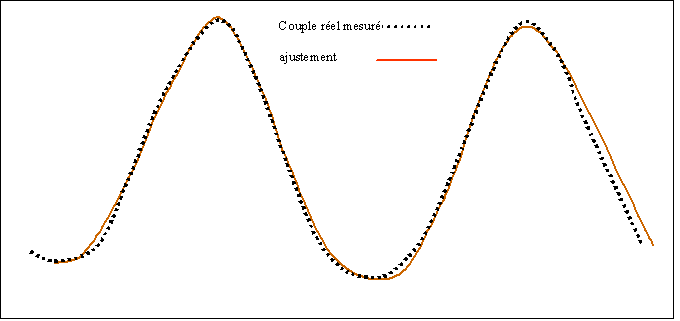
Fig.4a. Ajustement d’une courbe théorique à une courbe expérimentale avec n=3
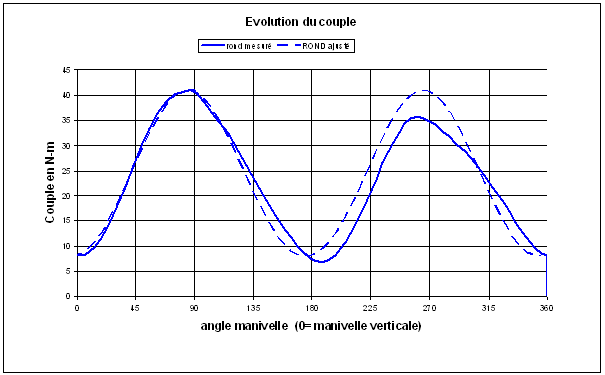
Fig.4b. Ajustement d’une courbe théorique à une courbe expérimentale avec n=2
(ne convient que pour une jambe, la seconde jambe exige un autre ajustement)
- La relation [3] permet d’exprimer le travail W du couple moteur au cours d’un demi-tour du plateau

On peut démontrer que les intégrales

sont égales, le travail s’écrit alors :
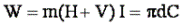
Avec n=2, on a: I=p/2 et avec n=3, on a: I=4/3
On montre donc que la somme H+V est constante pour un travail donné. Cela voudrait dire que si le cycliste veut modifier sa façon de pédaler, s’il diminue H, il devra augmenter V et vice-versa. Il n’est donc pas totalement libre.
Mettons un plateau ovale
Nous allons rentrer dans le vif du sujet en abordant les plateaux ovales.
La figure 4 représente un plateau elliptique c’est-à-dire ayant la forme d’une ellipse. Cette forme est surtout intéressante en ce qui nous concerne car elle peut être représentée par une équation unique.
La différence essentielle, sur le plan mécanique, avec un plateau circulaire est que le distance r’ varie en fonction de la position de la manivelle.
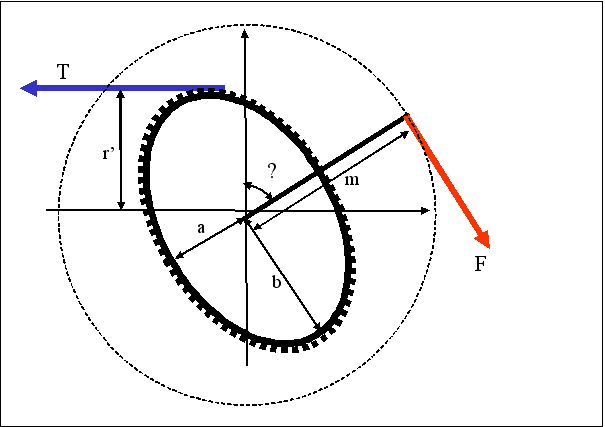
Fig.5. Plateau elliptique
a est l’axe de l’ellipse parallèle à la manivelle (pour θ =0, manivelle en haut, on a r’=a)
b est l’axe de l’ellipse perpendiculaire à la manivelle (pour θ =90 degré, on a r’=b)
La valeur de r’ est donnée par la relation :
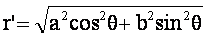
Dans la suite de nos calculs, nous comparerons un plateau circulaire avec des plateaux ovales ayant tous le même développement. Pour conserver le même développement, donc le même nombre de dents sur le plateau, il faut que le périmètre de l’ellipse soit égal au périmètre du plateau circulaire. Si le périmètre d’un cercle est donné par une formule stricte (2 πr), le périmètre d’une ellipse est donné par des formules approchées comme par exemple :
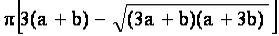
Pour un périmètre donné p, si l’on se fixe la valeur de a, la valeur de b sera donnée par :
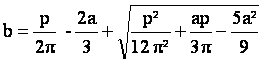
Nous utiliserons dans la suite un plateau de 52 dents. On rappellera que la distance entre deux dents ou deux maillons d’une chaîne est de 1,27 cm (1/2 pouce). Un plateau circulaire a alors un rayon de 105 mm. Si l’on choisit pour le plateau elliptique un demi grand axe de 110 mm, le demi petit axe doit être obligatoirement de 100 mm.
Le tableau 1 donne des géométries différentes compatibles pour 52 dents.
Tableau 1. Géométries admissibles d’un plateau elliptique pour 52 dents (en mm)

Le problème que l’on va chercher à résoudre est celui-ci :
Reprenons le test ergo-cycle et remplaçons le plateau circulaire par un plateau ovale ayant le même nombre de dents afin de conserver le même développement. Faisons un test avec la même valeur du couple résistant et la même vitesse (et donc la même cadence de pédalage) donc en conservant la même valeur du travail effectif. Comment le cycliste va-t-il réagir ? Quel va être son nouveau rythme de pédalage ? Va-t-il garder la même force F ou va-t-il la modifier ?
Il est certain que la réponse à ces questions se situe avant tout dans la tête et les jambes du cycliste et non pas dans la résolution d’équations mathématiques. C’est donc le résultat du test qui apportera les réponses.
Néanmoins, le fait d’imposer des contraintes au cycliste : même vitesse, même travail fourni, va conduire à quelques conséquences prévisibles.
Conséquence 1. Vérification de la validité des tests.
Comme on l’a vu, les tests sont réalisés en fournissant toujours le même travail. Sur le graphique de pédalage, le travail fourni au pédalier est donné par la relation [2]:
Cette intégrale représente l’aire définie par la courbe de pédalage et l’axe horizontal. Les aires relatives à chaque graphique doivent donc être égales que le plateau soit circulaire ou ovale.
Il importe donc de vérifier après chaque test que cette condition est réalisée. Si cela n’est pas le cas, il faut en déduire que le cycliste n’a pas pu respecter la contrainte sur la vitesse qui lui a été imposée. Le test doit alors être refusé sinon on comparera des choses qui ne sont pas comparables.
Conséquence 2. Vitesse angulaire
Les tests –plateau circulaire ou plateau ovale- sont réalisés en maintenant au mieux la vitesse constante mesurée sur la roue arrière, ce qui s’exprime en disant que la vitesse angulaire du pignon arrière est constante. Comme dans chaque test, le plateau a le même nombre de dents, la cadence de pédalage, c’est-à-dire le nombre de tours par seconde, reste aussi toujours la même.
Il s’ensuit qu’avec un plateau circulaire, la vitesse angulaire du plateau est également constante.
En revanche, la vitesse angulaire d’un plateau ovale n’est pas constante et varie lors d’un tour de manivelle.
En effet, désignons par :
ω la vitesse angulaire avec un plateau circulaire
ω’ la vitesse angulaire avec un plateau ovale
La vitesse de rotation du pignon restant constante au cours du test, la vitesse linéaire de la chaîne doit également rester constante. Cette vitesse linéaire au contact du plateau et de la chaîne est égale à :
ω r pour le plateau circulaire
ω’r’ pour le plateau ovale
On en déduit donc :
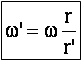
r’ étant fonction de la position de la manivelle lors de sa rotation,ω' est donc variable et inversement proportionnelle à r’.
Avec un plateau ovale, si l’on veut que la vitesse de rotation du pignon arrière reste constante, la vitesse angulaire instantanée de la manivelle est donc plus élevée lorsque la manivelle est verticale (aux points morts) et moins élevée pour la position horizontale.
La figure 6 illustre cette variation de vitesse pour différents plateaux ovales : un plateau elliptique (a=95 mm et b=115 mm) et deux autres plateaux qui seront présentés par la suite. La vitesse de rotation est de 60 tours/minute soit 6,28 rad/s.
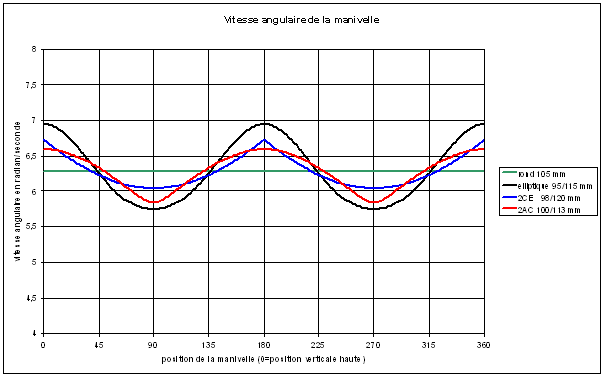
Fig.6. Variation théorique de la vitesse angulaire avec différents plateaux ovales.
Conséquence 3 : impact sur le graphique de pédalage
Soit F la fonction représentant la force exercée par le cycliste durant un test avec un plateau circulaire.
Soit F’ la même fonction concernant le test avec un plateau ovale.
L’égalité du travail fourni dans les deux tests est représentée par la relation [4]: :
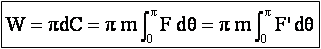
Appliquons cette relation à deux modèles de pédalage.
Application 1
Supposons un cycliste extra-terrestre qui serait capable d’exercer uniquement un effort constant F sur la manivelle donc totalement indépendant de la position de la manivelle.
F et F’ étant alors des constantes, la relation [4] devient :
F=F'
Le cycliste ne modifierait en rien sa façon de pédaler quel que soit le plateau. Il n’aurait aucun choix.
Application 2
Reprenons la relation [3] qui définit la fonction F dans le cas d’un plateau circulaire. On a donc :
F= H |cosnθ| + V sinnθ
Faisons l’hypothèse qu’en changeant de plateau, cette fonction reste représentative de la force F’ que le cycliste va alors exercer sur la manivelle. On aura:
F’= H’ |cosnθ| + V’ sinnθ
l’exposant n étant supposé rester constant, le cycliste a, à priori, deux degrés de liberté pour adopter un autre rythme de pédalage en jouant sur H et V.
La relation [4] devient :
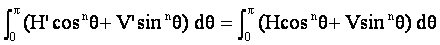
Ce qui s’écrit :
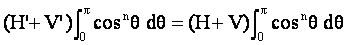
d’où
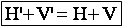
Cette relation ne permet pas à elle seule de déterminer les deux inconnues H’ et V’. Elle indique que la somme H’+V’ doit rester constante. Autrement dit, avec un plateau ovale, le cycliste aura la liberté de faire varier H d’une valeur Δ à condition de faire varier V de la valeur –Δ. Le cycliste n’a donc plus qu’un degré de liberté.
En pratique, il paraît évident qu’il choisira de diminuer H et d’augmenter V, puisque la difficulté pour un cycliste c’est la force H.
Les graphiques de pédalage obtenus lors de tests avec des plateaux ovales doivent se déduire des tests avec un plateau circulaire en diminuant H d’une valeur Δ et en augmentant V de la même valeur. Les tests doivent confirmer ou infirmer ces hypothèses sur la modélisation proposée pour la fonction de pédalage.
Les figures 7 présentent des ajustements de la fonction [3] à des tests de comparaison entre plateau circulaire et plateau ovale. La validité des tests a été vérifié par le calcul des aires définies par les deux courbes expérimentales : pour la figure 7a, on trouve une différence de 1,2 % entre l’aire obtenue avec le plateau circulaire et l’aire obtenue avec le plateau ovale, ce qui paraît fort satisfaisant, tandis que pour les graphiques de la figure 7b, on trouve une différence de 2,7 %, ce qui est moins bon.
Quant aux ajustements, ils semblent assez satisfaisants.
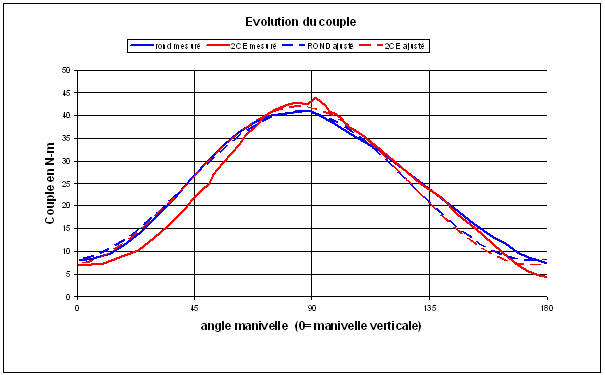
Fig.7a. Ajustement avec H+V=288 N et n=2
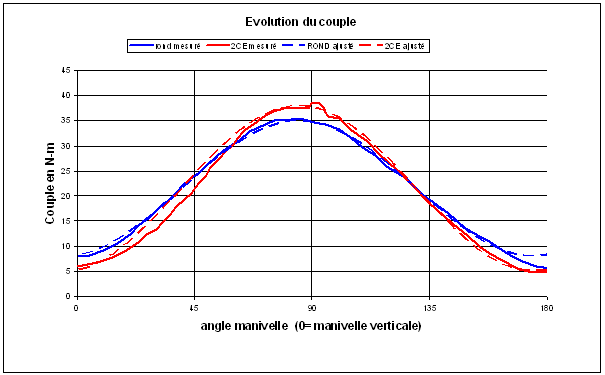
Fig.7b. Ajustement avec H+V=253 N et n=2
Quelle peut être la valeur de Δ ? Il nous manque une seconde équation reliant H’ et V’ pour que le problème ait une solution unique. A ce jour, nous n’avons pas d’idée sur le réflexe que pourrait avoir un cycliste et qui le conduirait à adopter plus ou moins inconsciemment telle ou telle valeur de Δ.
Autres formes de plateau
On peut imaginer de donner à un plateau la forme de son choix. Nous examinerons deux autres formes d’ovale basées sur des cercles et qui ont l’avantage de pouvoir être représentées par des fonctions analytiques.
Forme constituée par deux arcs de cercle
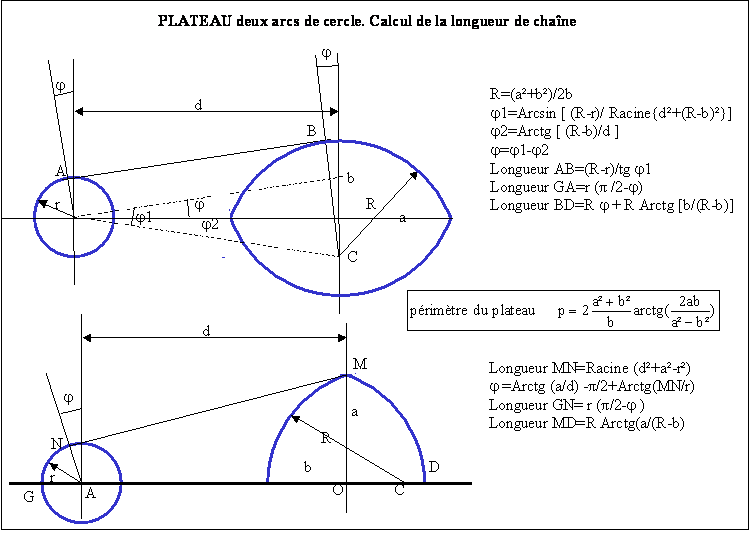
Cette forme de plateau est celle des plateaux commercialisés sous la marque « Ogival » (http://www.ogivalring.com). Elle est constituée par deux arcs de cercle comme le montre la figure 6.
Le calcul de la distance r’ est un peu plus complexe car celle-ci n’est pas régie par une seule équation.
On désignera par :
a la valeur du grand demi-axe du plateau
b la valeur du petit demi-axe du plateau.
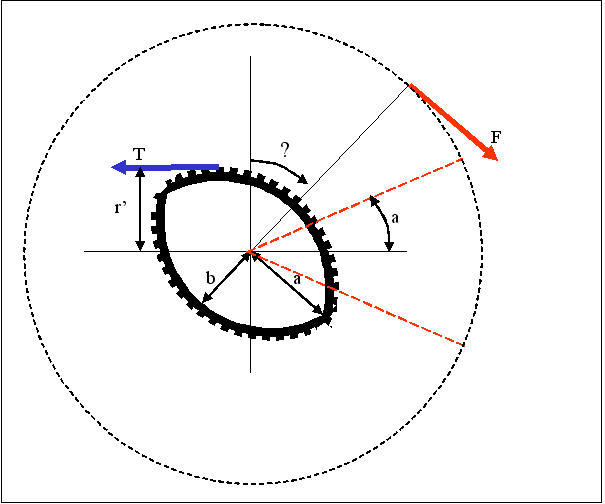
Fig.8 Plateau en arcs de cercle
A partir de ces deux paramètres, on peut calculer le rayon des deux arcs de cercle qui est égal à :
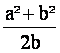
Il existe un angle α caractérisant ce plateau défini par :
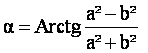
Cet angle correspond au mécanisme suivant : lorsque la manivelle se trouve dans le secteur d’angle 2α défini sur la figure 8, la chaîne ne s’enroule plus sur le plateau mais reste accrochée aux mêmes dents.
En positionnant la manivelle suivant le petit axe du plateau, lorsque la manivelle passe de la position haute à la position basse, c’est-à-dire lorsque l’angle θ varie de 0 à 180 degré, la valeur de r’ est donnée par les relations écrites ci-après :
Pour θ<90- α et pour θ>90+α
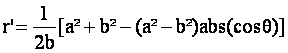
Pour 90- α < θ < 90+α
r'=a sin θ
Par ailleurs, le périmètre du plateau est égal à :
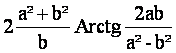
Comme pour l’ellipse, pour un plateau dont le nombre de dents est fixé, les valeurs de a et b sont liées entre elles. Dans le tableau 2, on donne des combinaisons admissibles pour un plateau de 52 dents :
Tableau 2. Géométrie d’un plateau en arcs de cercles pour 52 dents

On remarquera que l’ovalisation est plus prononcée avec ce type de plateau qu’avec un plateau elliptique.
Forme constituée par deux demi-cercles écartés
Il est constitué par deux demi-cercles de rayon a écartés l’un de l’autre d’une distance 2e. Les plateaux commercialisés sous le nom de « O’Symétric » n’ont pas strictement cette forme mais une forme qui s’en rapproche un peu.
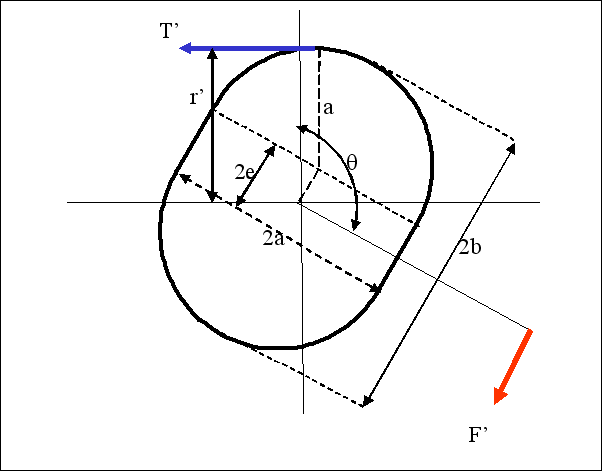
Fig.9. Plateau en deux demi-cercles
Si 2a est le petit axe du plateau et 2b le grand axe, l’écartement 2e est de 2b-2a.
Le périmètre du plateau est égal à 2πa +4(b-a)
La valeur de r’ est donnée par : r’=a +e sinθ
Tableau 3. Géométries admissibles d’un plateau en cercles écartés 52 dents

La puissance
Comme chacun doit le savoir, la puissance, c’est le travail effectué par unité de temps. Elle s’exprime en watt.
Pour un couple, la puissance est égale à la valeur du couple (en N-m) multiplié par la vitesse angulaire (en rad/sec). Elle s’écrit donc dans notre cas :
P=mF ω
Comme la force F varie en permanence en fonction de la position de la manivelle, si la vitesse angulaire reste constante, on voit que la puissance varie en permanence. C’est pourquoi, il faut bien distinguer :
- la puissance moyenne. C’est la puissance que l’on peut calculer durant un certain intervalle de temps, par exemple un tour de pédalier ou bien durant toute la durée d’un test ou d’un parcours routier.
- la puissance instantanée. C’est la puissance que l’on peut calculer en un instant précis et qui peut être fournie seulement durant une fraction de seconde. C’est le cas du pédalage où la puissance instantanée peut varier au cours de chaque tour de pédale.
En conséquence, lorsque l’on parle de puissance dans un système où force et vitesse varie, il faut bien préciser de quelle puissance il s’agit.
Dans le cas qui nous intéresse, le test de comparaison entre deux types de plateau, le couple résistant et la vitesse étant maintenus constants durant la durée de l’essai, la puissance moyenne reste la même dans tous les tests.
Quant à la puissance instantanée, elle varie en fonction de l’angle de la manivelle, que le plateau soit circulaire ou ovale.
Ainsi, lors d’un test avec le plateau circulaire, la puissance instantanée est égale à :
P=mF ω= m ω ( H |cosnθ| + V sinnθ)
et celle obtenue avec un plateau ovale est égale à :
P’=mF’ ω’= m ω’ ( H' |cosnθ| + V' sinnθ)
On a vu précédemment que pour maintenir constante la vitesse linéaire du cycliste, la vitesse angulaire ω’ avec un plateau ovale et la vitesse ω avec un plateau circulaire devaient être liées par la relation :
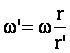
La puissance instantanée avec un plateau ovale est donc donnée par la relation :

Ainsi, pour un plateau elliptique, en remplaçant r’ par sa valeur en fonction de θ, on a la relation :
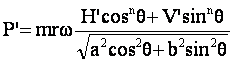
Cette fonction passe par un minimum pour θ=0 et pour θ=π , c’est-à-dire aux points morts.
Elle passe par un maximum pour θ= π/2 et pour θ=3π/2
Les valeurs de ces extrêmes sont :
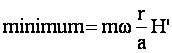
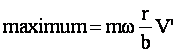
Il est intéressant de savoir si la puissance instantanée aux points morts avec un plateau ovale est supérieure ou non à celle avec un plateau circulaire. Pour cela, il faut que :
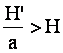
On voit que cette condition sera satisfaite si a est faible, c’est-à-dire si le plateau est très ovalisé et si H’ est fort. Cette dernière condition, au vu des tests, ne semble pas être remplie car H’ semble toujours inférieur à H.
Sur les figures 10 et 11, on a tracé des courbes de la puissance instantanée relatives à un plateau elliptique ainsi que la courbe concernant un plateau circulaire en adoptant les paramètres suivantes :
m=0,17
r=105 mm
a=90 mm
b=119 mm
ω= 60 tr/min=6.28 rad/s
H+V=280 N
Le travail fourni durant un tour est donné par W=mπ(H+V) soit, avec les données précédentes, W=149.5 Joules. La cadence étant de 1 tour par seconde, la puissance moyenne est donc de 149.5 Watts pour tous les cas présentés car la somme (H+V) a été maintenue constante.Sur la légende des graphiques, on a indiqué pour chaque courbe la valeur de H et la valeur de V.
Sur la figure 10, la puissance a été représentée en fonction de la position de la manivelle tandis que sur la figure 11 la puissance a été représentée en fonction du temps.
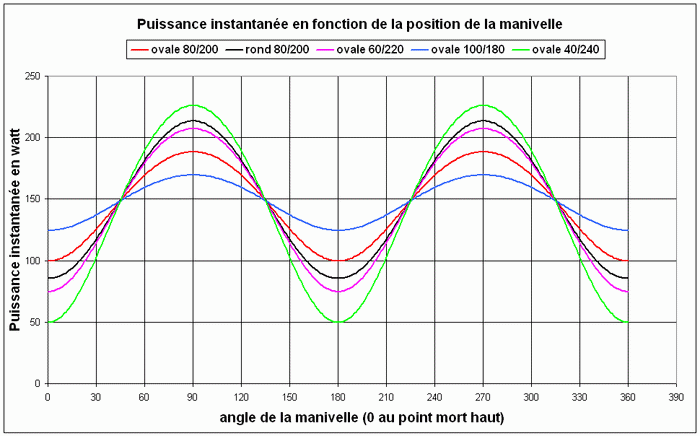
Fig.10. Puissance instantanée en fonction de la position de la manivelle
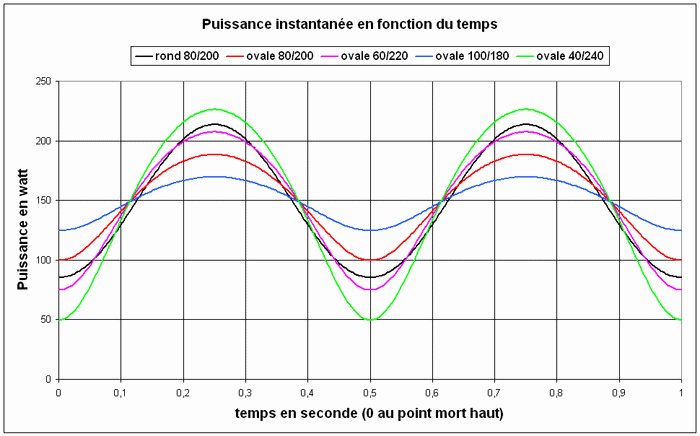
Fig.11. Puissance instantanée en fonction du temps
On en tire la conclusion, en comparant plateau circulaire et plateau ovale, que la puissance instantanée au moment où les manivelles sont horizontales est toujours inférieure dans le cas d’un plateau ovale. Aux points morts, la puissance instantanée peut théoriquement être supérieure ou inférieure avec un plateau ovale, cela est fonction de la force H. Les tests présentés dans ce document montrent que H est inférieur avec un plateau ovale.
Un plateau elliptique ne fournirait donc pas une puissance supérieure aux points morts.
Certains propos ou écrits sur les plateaux ovales laissent croire que les plateaux ovales apportent un gain de puissance, souvent sans préciser de quelle puissance il s’agit. S’il s’agit de la puissance moyenne, cela voudrait dire qu’il y a, lors d’un test, apport d’énergie entre le pédalier et la roue arrière, comme si un plateau ovale fonctionnait à la manière d’une assistance de VAE. De telles idées sont complètement erronées. S’il s’agit de la puissance instantanée, cela peut éventuellement être vrai mais c’est fort peu probable. Si un gain de performances peut être espéré, il faut chercher ailleurs l’explication comme on le verra ci-après.
Les performances
Pour répondre à la question que chacun se pose : « les plateaux ovales améliorent-ils les performances ? », il faut d’abord savoir comment évaluer une performance.
Pour pouvoir vaincre le couple résistant C, le cycliste doit fournir une certaine énergie. La performance peut alors s’exprimer par le rapport :
travail du couple C à la roue arrière/ énergie fournie par le cycliste
Plus ce rapport sera élevé, plus grande sera la performance. Pour une énergie donnée, plus le travail du couple sera important, plus grande sera la performance ou inversement, pour un travail donné, plus l’énergie fournie sera faible, plus grande sera la performance.
Pour faire une comparaison expérimentale de performances réalisées avec deux types de plateau, il faut reprendre le test-ergocycle avec le même protocole soit :
- maintenir constante la valeur du couple résistant durant la durée du test, ce qui est réalisé sur les home-trainers par un tambour sur lequel tourne la roue arrière du vélo et qui est associé à un frein
- maintenir constante la vitesse de rotation de la roue arrière : le cycliste doit régler son pédalage en surveillant le compteur affichant cette vitesse, ce qui induit également une cadence de pédalage constante
mais il faut le compléter par la mesure de l’énergie dépensée par le cycliste.
La mesure de cette énergie n’est pas aisée. Il faut bien voir que la mesure du couple au pédalier n’est pas la mesure de l’énergie dépensée par le cycliste car intervient le rendement du corps humain.
La mesure de l’énergie du cycliste peut se faire seulement indirectement :
- soit en mesurant le volume d’oxygène consommé durant la durée du test (VO)
- soit en mesurant la fréquence cardiaque. Cette mesure est moins précise car elle peut être influencée par d’autres facteurs que l’effort.
A ce jour, nous n’avons pas examiné avec suffisamment d’attention les résultats d’essais avec mesures de VO qui ont pu être publiés et ne pouvons donner une conclusion. A priori, nous ne pouvons pas exclure un meilleur rendement du corps humain, mais, pour analyser cela, il faut entrer dans la biomécanique, c’est-à-dire dans la mécanique du corps humain et non plus celle du vélo.
Tentative d’une explication biomécanique
L’idée part de la constatation évidente suivante : si l’on a tant de mal à passer par la position haute ou basse des manivelles, c’est que le corps humain a beaucoup plus de facilité à exercer avec la jambe un effort vertical qu’un effort horizontal. Cela peut se quantifier aisément par le test qui sera présenté ci-après.
Le mouvement de pédalage est un mouvement complexe où un nombre important de muscle intervient. Notre propos n’est pas de constituer un modèle mécanique de fonctionnement de tous ces muscles, ce qui est hors de notre compétence. Nous nous contenterons d’une analyse relativement simple.
Pour exercer un effort horizontal H durant un temps donné, le corps humain devra dépenser une énergie Eh que l’on estimera proportionnelle à la force H. On a donc :
Eh= kh H
De la même façon, pour exercer le même effort vertical V durant le même temps, le corps humain dépensera une énergie Ev :
Ev= kv V
avec kh > kv
Lors du mouvement de pédalage, le travail du couple étant proportionnel à H+V , ce travail sera inchangé, comme on l’a vu, si on diminue H d’une valeur Δ et si on augmente V de la même valeur Δ puisque :
(H - Δ) + (V + Δ) = H+V
En revanche, l’énergie que le corps devra fournir ne sera pas la même puisque :
- une diminution Δ de la force horizontale induira une diminution de la dépense énergétique égale à : δEh= kh Δ
- une augmentation Δ de la force verticale induira une augmentation de la dépense énergétique égale à : δEv= kv Δ
La variation de la dépense énergétique sera donc :
ΔEv - ΔEh= ( kv - kh ) Δ < 0
Il y aura donc, pour la même puissance moyenne fournie sur les pédales, une diminution de la dépense énergétique.
Pour moins se fatiguer, un cycliste devrait donc essayer de diminuer la poussée horizontale sur les pédales et augmenter la poussée verticale. Cette action peut théoriquement se faire quel que soit le plateau, même avec un plateau circulaire. La difficulté, c’est que cette action peut nécessiter des réflexes qui ne sont pas très naturels avec un plateau circulaire tandis qu’un plateau ovale pourrait la faciliter.
Pour vérifier cette hypothèse, nous avons effectué les expériences suivantes consistant à analyser séparément une poussée horizontale et une poussée verticale.
- Expérience 1. Analyse de la poussée verticale. Le montage A permet de faire des va-et-vient verticaux en soulevant un poids P1. On mesure la fréquence cardiaque. La fréquence cardiaque peut être en effet être considérée comme un indicateur de l’énergie dépensée tout en gardant en mémoire que beaucoup de facteurs, certains de nature psychologique, influe sur cette fréquence.
- Expérience 2. Analyse de la poussée horizontale. Même expérience suivant le montage B où l’on exerce une poussée horizontale P2.
Un protocole strict doit être respecté pour chacune de ces expériences qui doivent être répétées pour permettre une interprétation plus fiable.
7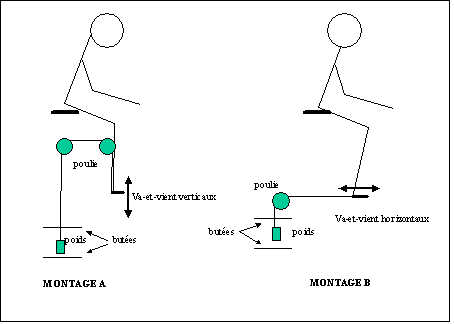
Fig.12. Analyse de l’effort vertical et de l’effort horizontal
Cette interprétation peut s’effectuer de la manière suivante :
On admettra que la fréquence cardiaque fc est liée aux forces H et V par la relation linéaire suivante :
fc = αH+ βV + γ
Pour déterminer les coefficients α ,β et γ, on a :
au repos : fc = fc0 H=0 V=0 d’où γ= fc0
avec l’expérience 1 : fc = fc1 H=0 V= P1 d’où β = (fc1- fc0)/P1
avec l’expérience 2 : fc = fc2 H= P2 V=0 d’où α = (fc2 -fc0)/P2
Application numérique. Des tests effectués avec P1=P2=6 kg ont donné :
fc0= 75 fc1 = 88 fc2=80
On en déduit : fc=2,17 H + 0,83 V + 75
Si maintenant, on diminue H et on augmente V d’une même valeur Δ , la variation de la fréquence cardiaque sera de :
δfc = -2,17 Δ + 0,83 Δ = - 1,34Δ < 0
Ainsi, en prenant Δ= 1 kg, la baisse de fréquence cardiaque sera de 1,34 pulsation/minute.
En conséquence, si l’on admet qu’un plateau ovale permet une réduction de la poussée horizontale et une augmentation de la poussée verticale par rapport à un plateau circulaire, on devrait, pour la même puissance fournie sur les pédales, aboutir à une très légère diminution de l’énergie dépensée par le corps humain.
Inversement, en conservant la même dépense d’énergie, il est intéressant d’évaluer la puissance additionnelle qui sera fournie sur les pédales et donc le gain de vitesse que l’on pourrait obtenir. Pour cela, il faut que le cycliste connaisse sa relation personnelle entre sa fréquence cardiaque et la puissance fournie, relation qui s’obtient dans un test d’effort. Personnellement, un tel test a permis de voir qu’une augmentation de 10 pulsation/minute permettait d’augmenter la puissance de 26 watts. Une augmentation d’une pulsation/minute correspondrait donc à une augmentation de puissance de 2,6 watt.
Que peut-on faire avec cette augmentation ? A partir des équations liant vitesse et puissance (voir « Le vélo en équation » sur le site du club), pour un cycliste de 70 kg qui roulerait à 30 km/h, on peut calculer que la puissance fournie sur les pédales est de 173,24 watts et qu ‘en ajoutant 2,6 watts, sa vitesse passerait à 30,19 km/h. Ce gain est certainement sans intérêt pour un cyclotouriste. Pour un professionnel, c’est peut-être toujours bon à prendre.
Un inconvénient du plateau ovale ?
Avec un plateau ovale, la longueur de la chaîne en position A1-A2 représentée sur la figure 13 n’est pas la même qu’en position B1-B2. La longueur A1-A2 est plus grande que la longueur B1-B2.
Cela veut dire que si on tendait une chaîne en position B1-B2, sans intercalation d’un dérailleur, on ne pourrait pas faire tourner le plateau. Il faut que la chaîne ait au moins une longueur A1-A2.
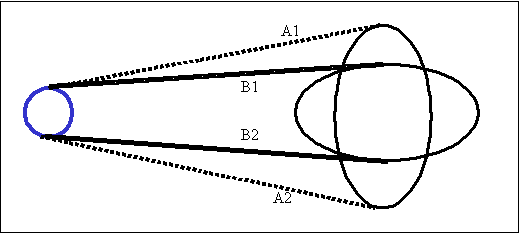
Fig.13. Variation de longueur de chaîne en fonction de la position de l’ovale.
La différence de longueur n’est cependant pas très grande, elle est de l’ordre du centimètre. Elle dépend de la forme du plateau. En annexe, nous donnons les relations permettant de calculer analytiquement la longueur de chaîne pour deux types de plateau : plateau constitué par deux arcs de cercle (type Ogival) et plateau ovale obtenu en écartant deux demi-cercles. Pour un plateau strictement elliptique, une résolution analytique est impossible, il faut faire une résolution numérique. Les formules permettant de faire cette résolution sont également présentées en annexe.
Le tableau ci-dessous donne les longueurs minimales de chaîne pour ces différents types de plateau en prenant les données suivantes :
nombre de dents du plateau 52
valeur de l’entraxe plateau-pignon 42 cm
rayon du pignon 2,3 cm (12 dents)
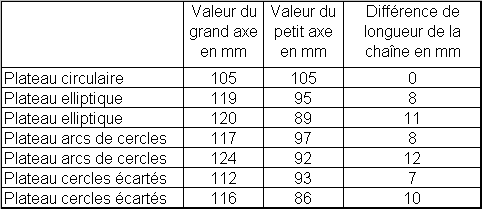
En adoptant une chaîne de longueur A1-A2 en l’absence de dérailleur et en tendant bien cette chaîne, lors du mouvement de pédalage, le brin inférieur va se détendre lorsqu’il passera en position B2.
En présence d’un dérailleur arrière, le ressort du dérailleur rattrapera le jeu et cela deux fois par tour complet de manivelle c’est à dire 120 fois par minute pour une cadence de pédalage de 60 tours/minute. Il peut en résulter des battements du brin inférieur qui risque d’engendrer des vibrations, ce qui, mécaniquement parlant, n’est pas souhaitable.
On n’oubliera pas non plus que les brins de la chaîne montent et descendent deux fois par tour de manivelle. Nous n’avons pas d’expérience pour dire si tous ces mouvements de la chaine sont gênants ou non et si le cycliste les ressent. Il serait intéressant de mieux analyser ce problème.
Conclusions
Que tirer comme conclusions de l'étude ?
- Sur l'aspect purement mécanique, si l'on compare un plateau ovale et un plateau rond, dans des conditions identiques : même développement, même cadence de pédalage, un plateau ovale diminue le travail effectué aux points morts mais par contre l'augmente aux points forts, c'est-à-dire lorsque la manivelle est dans une position pseudo-horizontale. Dans les deux cas, l'énergie ou la puissance à fournir au pédalier est évidemment strictement identique. Il ne faut pas s'imaginer que le plateau ovale fonctionne comme un VAE en fournissant une énergie supplémentaire.
- Sur l'aspect physiologique, le problème se pose comme suit : pour fournir une énergie mécanique au pédalier, le cycliste doit dépenser de l'énergie interne. La dépense d'énergie interne supplémentaire que l'on fait aux points forts avec un plateau ovale est-elle largement compensée par l'économie d'énergie que l'on fait aux points morts ? Ce n'est plus là évidemment un problème pouvant être résolu par voie mathématique, c'est de la bio-mécanique. Le mouvement de pédalage est produit par deux couples principaux : le couple exercé au niveau de la hanche (rotation entre le fémur et le bassin) et le couple exercé au niveau du genou (rotation entre le fémur et le tibia). Au point mort haut, c'est le couple genou qui travaille (extension de la jambe), au point fort, c'est le couple hanche qui travaille (extension de la cuisse). L'être humain est fait de telle sorte qu'il lui est plus facile d'exercer un effort par l'extension de la cuisse que par l'extension de la jambe. Le bilan d'énergie interne nécessaire pourrait donc être moindre en faisant travailler la cuisse plutôt que le genou : cela pourrait donc induire une dépense plus faible d'énergie interne pour fournir la même puissance au pédalier, à condition que l'économie d'énergie interne faite au point fort soit supérieure à la dépense supplémentaire d'énergie interne au point fort, donc cela produirait un avantage pour le plateau ovale.
Cependant, les hommes ne sont pas identiques, ce qui est bon pour l'un pourrait être moins bon pour l'autre. Cela ne peut être tranché que par voie expérimentale par des tests sur vélo ergocycle aptes à mesurer l'énergie interne dépensée. Ces tests sont malheureusement très indirects et risquent fort de manquer de précision : mesure de la fréquence cardiaque ou mesure de l'oxygène consommé lors d'un test dit « test d'effort ».- Le test de fréquence cardiaque peut être fait chez soi si l'on dispose d'un home-trainer avec enregistrement des paramètres. Le protocole suggéré est décrit dans le document « Détection d'une anomalie cardiaque ». Il a pour objectif d'établir la courbe puissance-fréquence cardiaque telle que celle représentée sur la figure 14. On comparera ensuite les courbes résultant de tests avec plateau rond et plateau ovale. Cependant, ce test risque d'être fort imprécis, la fréquence cardiaque pouvant être influencée par bon nombre de facteurs.
- La mesure de l'oxygène consommé lors de tests d'efforts nous paraît plus rigoureuse mais ne peut guère être réalisée chez soi, le matériel pour cela est trop spécialisé.
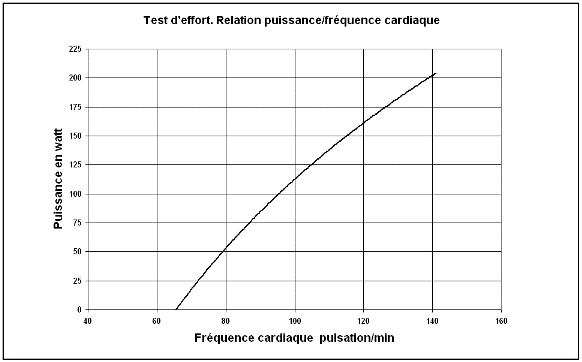
Fig.14. Relation puissance-fréquence cardiaque résultant d'un test d'effort.
Un test plus simple et global peut être fait en effectuant plusieurs fois un parcours donné avec un plateau circulaire puis un plateau ovale en maintenant toujours sa fréquence cardiaque à une valeur fixée et en regardant avec quel plateau on obtient la vitesse moyenne la plus élevée mais en pratique la différence étant si minime que la conclusion risque d'être faussée par des éléments extérieurs et l'imprécision des mesures.
Quant à la démonstration qui consiste à affirmer que le coureur X ou Y a gagné telle ou telle course et était équipé d'un plateau ovale, elle ne peut qu'être contestée par un esprit scientifique. Notamment, on ne dévoile jamais si le dernier de la course était aussi équipé d'un plateau ovale ou bien si seulement ce n'était pas les meilleurs coureurs qui en étaient équipés.
Quant à la sensation qu'éprouvent des adeptes des plateaux ovales cyclistes qui l'expriment en disant « on tourne plus rond », comment traduire en langage mathématique cette sensation d'un pédalage plus fluide ? Cela n'est pas du tout évident.
Une mécanique qui tourne rond, c'est une mécanique qui fonctionne très régulièrement, sans à-coups, avec des mouvements de rotation peu perceptibles : avec un plateau ovale, nous en sommes loin, ne serait-ce que l'irrégularité de la vitesse angulaire des plateaux. On serait à même d'affirmer le contraire : le plateau ovale devrait conduire à un pédalage heurté.
La sensation d'un pédalage plus fluide peut s'expliquer simplement par une meilleure adaptation à la force que le cycliste doit exercer à chaque instant sur la pédale pour vaincre le couple résistant : comme il a été dit, aux points morts, le cycliste ne dispose que d'une poussée horizontale faible, il faut donc que la force à exercer soit faible à ce moment là et l'inverse lorsque la manivelle est horizontale où le cycliste dispose d'une poussée verticale forte.
En conclusion, les sciences physiques et mécaniques ne peuvent pas établir une démontration imparable de l'avantage ou non des plateaux ovales et c'est vers le comportement bio-mécanique de l'être humain qu'il faut se tourner. Au vu de cette analyse, on peut comprendre pourquoi les plateaux ovales ne se sont pas systématiquement imposés et pourquoi les avis des utilisateurs sont extrêmement partagés et parfois contradictoires.
Références
[1] Thomas Lihoreau. Projet de fin d’études. « Analyse du geste de pédalage » 2007. Université de Franche Comté. Besançon
[2] Nicolas Rambier. Mémoire Master. « Effet de l’utilisation du plateau O’Symétric sur la performance du cycliste ». Université de Franche Comté.UPFR des Sports.Besançon. 2013
[3] Jacques Fine « Le vélo en équation » http://www.velomath.fr
ANNEXES
Bases pour le calcul de la longueur de chaîne
pour 3 formes de plateau
Plateau deux demis cercles
Plateau deux arcs de cercle
Plateau en ellipse
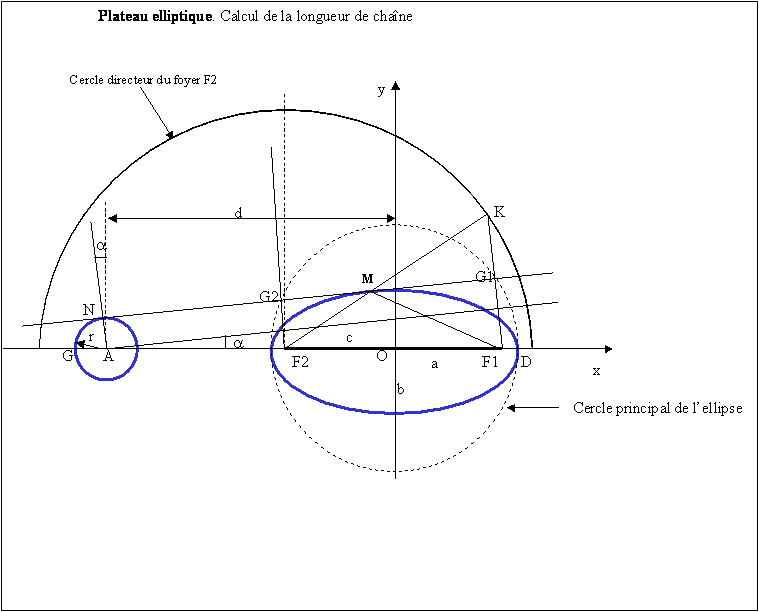
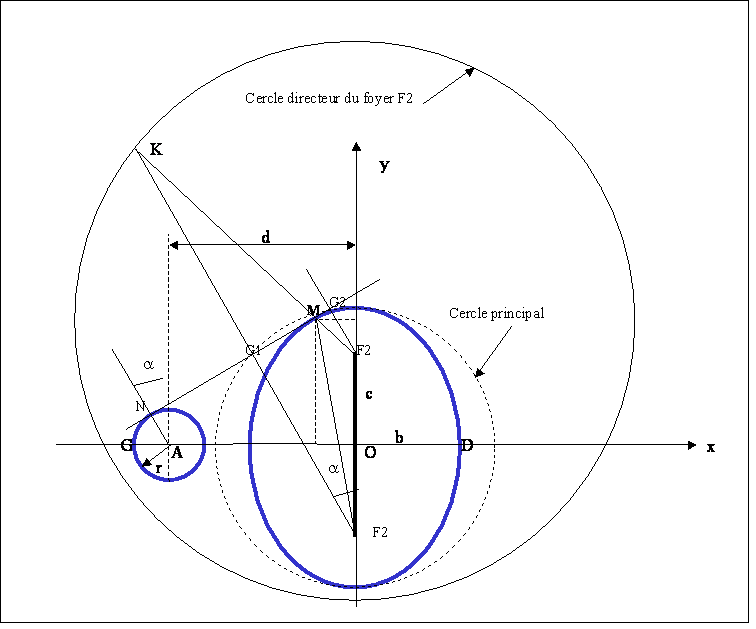
Notations pour le calcul du plateau elliptique :
a est le grand axe de l’ellipse
b est le petit axe de l’ellipse
F1 et F2 sont les foyers de l’ellipse
c=OF1=OF2
On a c²=a²-b²
MN est la tangente commune au cercle de rayon r (pignon) et à l’ellipse.
La détermination des coordonnées du point de contact M se fait en utilisant la propriété suivante de la tangente à une ellipse : la perpendiculaire à la tangente menée à partir du foyer F1 coupe la tangente en un point G1 (x1,y1) qui se trouve sur le cercle principal de l’ellipse de rayon a et coupe le cercle directeur relatif au foyer F2 en un point K. G1 est le milieu du segment F1K. Le point de contact M (xm, ym) se trouve sur la droite F2 K.
La résolution ne peut se faire que par méthode numérique. Dans les deux tableaux, on donne le système d’équations à résoudre dans les deux configurations: grand axe horizontal et grand axe vertical.
La détermination de la longueur de l’arc MD ne peut également se faire que par méthode numérique.