A quelle vitesse aborder un virage ?
Février 2016
contact@velomath.fr
Négocier correctement un virage reste une opération délicate pour un cycliste lorsque la vitesse est élevée car il doit coordonner plusieurs actions : contrôler sa trajectoire avec le guidon, se pencher vers l’intérieur du virage, jouer sur les freins pour ajuster sa vitesse.
Cette situation se présente notamment dans les descentes des cols où il est évident qu’un virage en épingle à cheveu ne peut pas être abordé à n’importe quelle vitesse.
Nous allons donner une formulation mathématique à ce problème.
Vitesse limite dans un virage
Nous admettrons que le cycliste de masse M effectuant un virage de rayon de courbure R est animé d’un mouvement circulaire uniforme à la vitesse V. Les forces mises en jeu sont :
- le poids du cycliste et du vélo W
- la force centrifuge Fc qui est donnée par la relation :
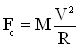
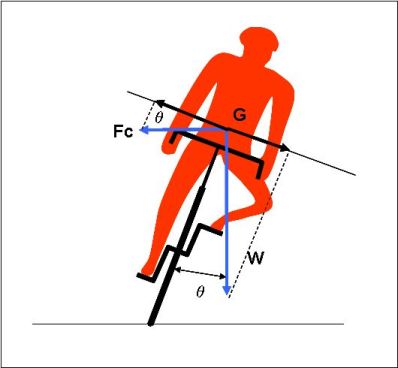
Fig.1. Forces en présence
Pour ne pas être déporté vers l’extérieur du virage, le cycliste doit se pencher vers l’intérieur afin de créer une composante du poids équilibrant la force centrifuge. On doit donc avoir :
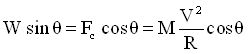
Comme on a W=Mg (g étant l’accélération de la pesanteur g=9.81 m/s²), la relation s’écrit simplement :
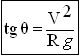
Cette relation donne donc l’angle d’inclinaison du cycliste nécessaire pour que le cycliste reste dans sa trajectoire. Cet angle dépend de la vitesse et du rayon de courbure du virage. Le tableau à double entrée ci-dessous donne des valeurs de cet angle.
Tableau 1.
Inclinaison θ en degré en fonction du rayon de courbure et de la vitesse
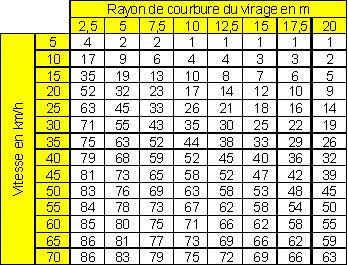
Cette condition est nécessaire mais pas suffisante pour assurer la stabilité du cycliste. En effet, il y a un risque de glissement des pneus sur la chaussée. Pour éviter ce risque, il faut que la relation suivante soit satisfaite :
Fc < W tg φ
tg φ étant le coefficient de frottement entre les pneus et la chaussée
On obtient donc la seconde condition nécessaire :
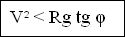 |
Equation [1] |
La valeur de l’angle de frottement est souvent pris égale à 0.8 pour une chaussée normale et à 0.4 pour une chaussée mouillée.
La figure 2 donne la vitesse limite en fonction du rayon de courbure et de l’angle de frottement pneu-chaussée.
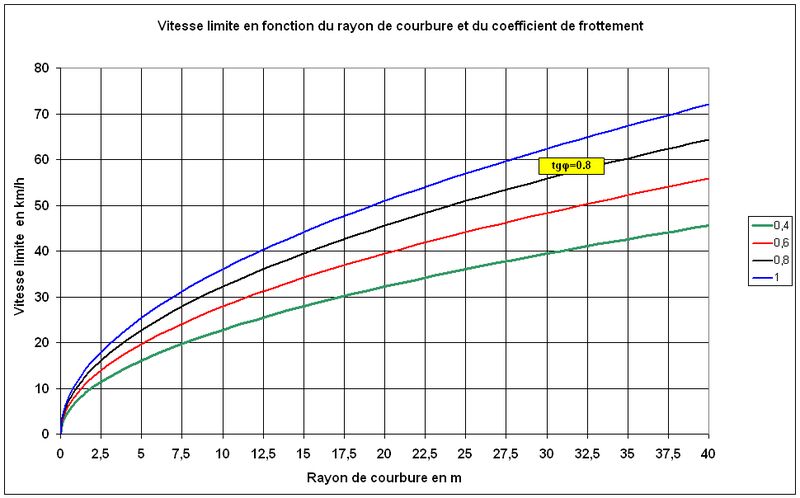
Fig.2. Vitesse limite dans les virages
Rayon de courbure
Quel est l’ordre de grandeur des rayons de courbure en montagne ? La figure 3 est une photo aérienne de l’un des 21 virages de la montée de l’Alpe-d’Huez. Sur cette photo, on a ajusté deux demi-cercles. Le cercle correspondant au virage intérieur a un rayon de 4.2 m et celui du virage extérieur est de 11.5 m. Ces valeurs sont dans l’ordre de grandeur des rayons de courbure des virages en épingle à cheveu : de 2 à 5 m pour le rayon intérieur et de 8 à 12 m pour le rayon extérieur.

Fig.3. Rayon de courbure
Coefficient de sécurité
En pratique, il n’est pas raisonnable de s’approcher de la vitesse limite car nombre d’aléas peuvent survenir, par exemple l’état de la chaussée. Il faut garder une marge de sécurité. De façon identique à ce qui est fait en mécanique, on définira un facteur de sécurité fs comme étant le rapport entre les forces résistantes et les forces motrices.
Ainsi, dans notre problème, la force résistante qui s’oppose au dérapage est W tg φ
La force motrice qui produit le dérapage est Fc.
Le coefficient de sécurité est fs=W tg φ/Fc soit :
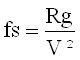
A l’équilibre limite, le facteur de sécurité est égal à 1. Si ce facteur est supérieur à 1, la stabilité est assurée. S’il est inférieur à 1, c’est la chute immédiate.
On adoptera donc une vitesse égale à :
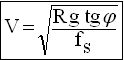
Il paraît raisonnable d’opter pour un facteur de sécurité de 2.
Les courbes de la figure 4 donnent alors la vitesse à adopter.
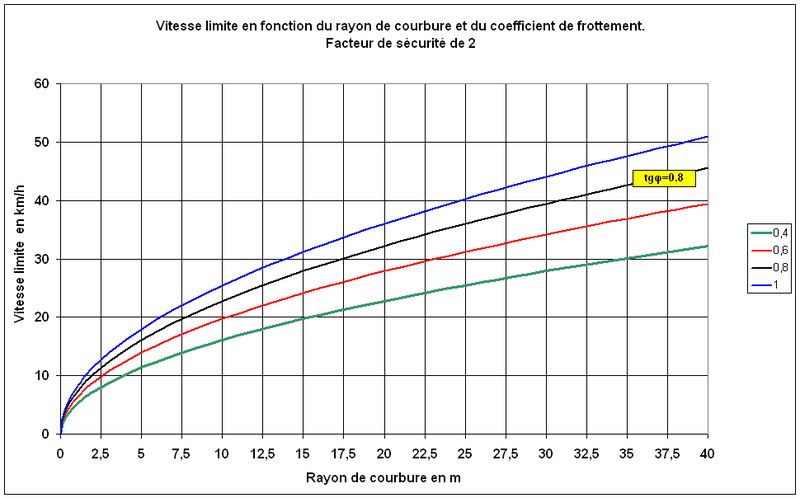
Fig.4. Vitesse sécuritaire
Virages relevés ou en dévers
La relation [1] a été établie en admettant que le profil transversal de la route est horizontal. En réalité, les virages sont la plupart du temps relevés afin de faciliter les manœuvres des usagers.
Désignons par i l’inclinaison du profil (voir figure 5).
Au contact pneu-chaussée:
la force perpendiculaire à la chaussée est : Wcos i+ Fc sin i
la force tangentielle est : Fc cos i – W sin i
Tout calcul fait, la relation [1] devient :
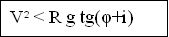 |
Equation [2] |
Tout se passe donc comme si le coefficient de frottement pneu-chaussée augmentait. Ainsi, si l’angle de frottement est de 40 degré, donc un coefficient de frottement tg φ égal à 0.84, un profil de chaussée penté à 5 degré correspondra à un angle de frottement de 40 +5= 45 degré soit un coefficient de 1.
On rencontre parfois, mais cela est heureusement très rare, des profils de virage en dévers c’est-à-dire incliné vers l’extérieur du virage. Cette situation sera lors assimilable à une diminution du coefficient de frottement donc préjudiciable à la bonne prise du virage.
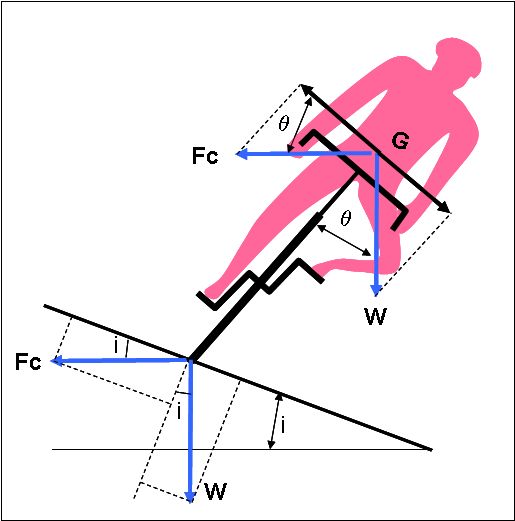
Fig.5. Virage relevé
Changement de trajectoire
On a vu que la force centrifuge était inversement proportionnelle au rayon de courbure R, ce qui entraîne que le facteur de sécurité est proportionnel à R. Aussi, si le cycliste modifie brutalement le rayon de courbure en donnant un coup de guidon, le coefficient de sécurité va également varier. En réduisant de moitié, par exemple, le rayon de courbure, ce qui peut arriver pour éviter de sortir de la route, le coefficient de sécurité va être divisé par deux. Si ce coefficient ne dépassait guère 1, il tombera à moins de 1 après le coup de guidon, c’est le dérapage immédiat.
La meilleure trajectoire
Légalement, le problème du choix de la meilleure trajectoire ne se pose pas pour un cycliste ordinaire puisqu’il doit respecter le code la route et donc rouler à droite. Dans la descente d’un col, il prendra successivement des virages intérieurs et des virages extérieurs. Par contre, le coureur a plus de choix puisque la route lui est réservée.
La figure 6 schématise un virage en épingle à cheveu. Sur cette figure, on a tracé 3 trajectoires.
- la trajectoire 1 où le virage est pris entièrement à l’intérieur
- la trajectoire 2 où le virage est pris entièrement à l’extérieur
- la trajectoire 3 où le virage est intermédiaire.
Quelle est la trajectoire la plus rapide ?
La distance AA’ de la trajectoire 1 est nettement plus faible que la distance BB’ de la trajectoire 2 mais la vitesse de 2 est plus grande que la vitesse de 1. Qui l’emporte ?
Les temps t1 et t2 mis pour parcourir respectivement AA’ et BB’ sont donnés par :
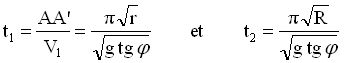
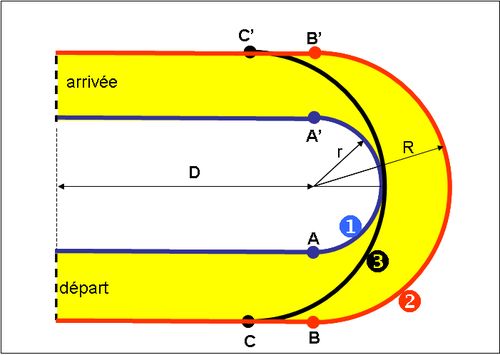
Fig.6. Schématisation de trajectoires
Ils sont donc proportionnels à la racine carrée du rayon de courbure. Dans l’exemple du virage de l’Alpe-d’Huez, on aurait t1= 2.28 secondes et t2=3.80 secondes.
La trajectoire 1 serait donc plus rapide. On gagnerait 1.52 secondes.
Cependant, ce calcul est incomplet. En effet, il faut tenir compte de « l’avant virage » et de « l’après virage ». La trajectoire 1 nécessite de freiner plus fort avant le virage et de relancer plus fort après le virage, d’où une perte de temps avant et après le virage.
Pour tenir compte de ces phases, on s’est livré à une simulation numérique des trois trajectoires.
Simulation
Les conditions de simulation sont les suivantes :
- la route est une descente pentée à 8%. La simulation est faite entre une ligne « départ » et une ligne « arrivée » qui se situent à D=100 m du virage
- les rayons de courbure du virage sont ceux du virage de l'Alpe-d’Huez pris en exemple, soit 4.2 m et 11.5 m
- les cyclistes ne fournissent aucune puissance de pédalage car ils sont en roue libre
- ils franchissent la ligne « départ » à la vitesse de stabilisation pour une descente en roue libre soit 60.8 km/h
- ils prennent les virages à la vitesse maximale (équation [1]), donc sans aucun facteur de sécurité. la vitesse V1 est de 20.7 km/h, les vitesses V2 et V3 sont de 34.2 km/h. On peut calculer que les temps mis pour prendre le virage sont respectivement de 2.28 et 3.80 secondes.
- ils freinent avec la force maximale, à la limite de la chute, donc sans facteur de sécurité (voir le document « Le freinage en équation »). Le calcul de l’opération de freinage donne les résultats suivants:
- la force de freinage maximale est de 412 N.
- pour passer de 60.8 km/h à 20.7 km/h, le cycliste 1 parcourra une distance de 26 m en 2.35 secondes. Il commencera donc son freinage après avoir parcouru 100-26= 74 m
- pour passer de 60.8 km/h à 34.2 km/h, les cyclistes 2 et 3 parcourront une distance de 20 m en 1.55 secondes. Le cycliste 2 commencera à freiner au bout de 80 m et le cycliste 3 freinera après 72.7 m.
- à la sortie du virage, les cyclistes ne relancent pas, ils relâchent les freins et sont en roue libre jusqu’à la ligne d’arrivée. Le calcul du temps pour parcourir la distance entre la sortie du virage et la ligne arrivée aboutit à :
- cycliste 1 : 100 m parcouru en 11.4 secondes et arrivée à 40.9 km/h
- cycliste 2 : 100 m parcouru en 8.9 secondes et arrivée à 46.14 km/h
- cycliste 3 : 92.7 m parcouru en 8.3 secondes et arrivée à 45.5 km/h
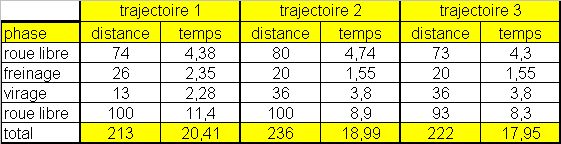
Les distances des différentes phases et le temps mis pour les parcourir sont rassemblés dans le tableau 2. On constate que la trajectoire la plus rapide est la trajectoire 3. La trajectoire la moins rapide est finalement la trajectoire 1 bien que ce soit celle-ci qui permette de passer le virage le plus rapidement. La trajectoire 3 permet de gagner environ 2.5 secondes par virage par rapport à la trajectoire 1. Sur 21 virages, l’avance sera donc de 52 secondes entre un bon descendeur et un mauvais descendeur.
Tableau 2. Bilan de la simulation
Conclusions
Prendre un virage avec une vitesse élevée est une opération à risques. Le cycliste devra trouver sa bonne inclinaison par rapport à la verticale pour suivre la trajectoire prévue et agir sur les freins avant le virage sans risquer de déraper ou de culbuter afin de régler correctement sa vitesse.
Si l’on veut gagner des secondes, la vitesse doit se rapprocher de la vitesse limite, la force de freinage doit, sans les dépasser, se rapprocher des forces limites au delà desquelles la chute ou perte de direction est certaine. Ces valeurs limites dépendent de paramètres assez aléatoires pouvant changer d’un virage à l’autre tels que : état de la chaussée, chaussée relevée dans le virage, rayon de courbure du virage. En une fraction de secondes, le cycliste doit intégrer ces paramètres et agir en conséquence. Le droit à l’erreur n’est pas possible, corriger sa trajectoire en diminuant le rayon de courbure risque fort de conduire au dérapage car la vitesse sera trop élevée pour un rayon plus faible, la corriger en augmentant le rayon risque de provoquer une sortie de route, freiner trop fort conduira aussi au dérapage. On comprend alors pourquoi, dans le domaine de la course cycliste, on parle de bons et de mauvais descendeurs mais parfois ne faudrait-il pas parler de conscients et d'inconscients.
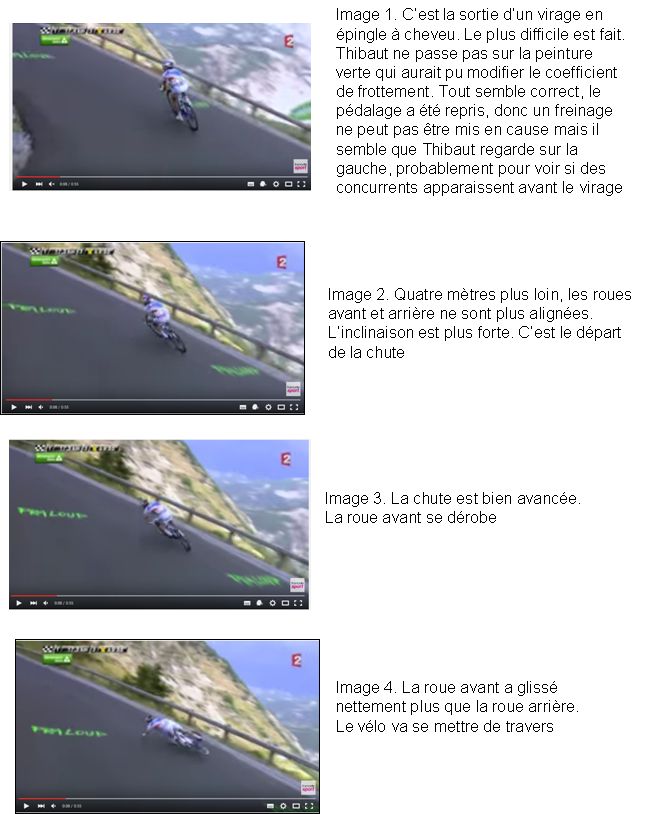
Lors du Tour de France 2015, on a beaucoup parlé de la chute de Thibaut Pinot, plus décevante pour l’intéressé que grave car ce dernier pouvait prétendre à la victoire d’étape. L’examen de la vidéo publiée sur Internet et dont sont extraites les images suivantes semblent montrer que c’est un changement de trajectoire qui a provoqué cette chute. Une réduction du rayon de courbure a augmenté la force centrifuge. La roue avant et non pas la roue arrière a glissé vers l’extérieur, ce qui peut s’expliquer par le fait que le coureur qui avait repris le pédalage après le virage négocié en roue libre, était en phase d’accélération et donc le poids s’est reporté sur la roue arrière et a déchargé la roue avant, favorisant son dérapage. Le changement de trajectoire est probablement dû à la perte du contrôle rigoureux de cette trajectoire provoquée par le détournement du regard.