Sur un parcours en « montagnes russes » où les montées abruptes succèdent aux descentes tout aussi abruptes, le cycliste pessimiste ne pensera qu'à l'effort qu'il devra fournir pour la montée alors que le cycliste optimiste appréciera la descente qui lui permettra de prendre suffisamment d'élan pour que la remontée se fasse sans grand effort.

Qu'en est-il exactement ?

Nous allons demander aux mathématiques de répondre aux questions suivantes :

La réponse à ces questions exige des connaissances mathématiques dont le niveau est supérieur à celui du bac scientifique. Que le lecteur ne se décourage pas, il peut sauter les calculs présentés dans les paragraphes « résolution » et aller directement aux paragraphes « applications »

Descendre en roue libre

Tous freins lâchés, dans une descente, le cycliste va prendre de la vitesse mais cette vitesse va pratiquement se stabiliser car hélas la résistance de l'air augmente vite avec la vitesse si bien qu'elle va atteindre la valeur de la force de pesanteur qui attire le cycliste vers le bas. Il va y avoir une vitesse limite que nous appellerons Vs que le cycliste ne pourra pas dépasser.

Sachant que le cycliste aborde la descente avec une vitesse initiale égale à V0, nous allons maintenant chercher à calculer le temps et la distance nécessaire pour atteindre la vitesse limite.

Nous adopterons comme unités les unités légales et non pas les unités utilisées par les cyclistes soit le poids en Newton, la distance en m, le temps en secondes et la vitesse en m/s. Cela a l'avantage de simplifier l'écriture des équations.

Adoptons les notations suivantes:

Résolution

Si le cycliste est en roue libre, la vitesse limite Vs s'obtient en prenant l'équation donnant la puissance à fournir par un cycliste pour avancer à une vitesse V (équation établie dans le document « Le vélo en équation ») et en écrivant que la puissance fournie par le cycliste dans la descente est nulle, soit :

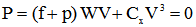équation [1]

D'où l'on tire :

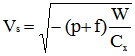Avec les conventions adoptées, la pente d'une descente est négative et donc le terme sous le radical est positif.

Sachant que le cycliste aborde la descente avec une vitesse initiale égale à V0, nous allons maintenant chercher à calculer le temps et la distance nécessaire pour atteindre la vitesse limite.

Avec les unités adoptées, l'équation fondamentale de la dynamique f=mγ appliquée à l'ensemble cycliste et vélo s'écrit :

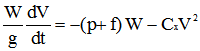équation [2]

En posant:
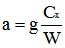cette équation peut s'écrire:

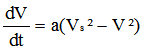Sachant qu'au temps t=0 où le cycliste entame la descente, la vitesse est égale à V0, l'intégration de cette équation dont nous vous épargnerons les détails conduit à la relation ci-après reliant la vitesse au temps nécessaire pour atteindre cette vitesse:

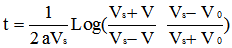équation [3]

De cette relation, on peut tirer la vitesse V, soit :

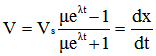équation [4]

après avoir posé:

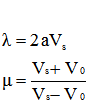Sachant qu'au temps t=0, la distance parcourue en descente est égale à 0, l'intégration de cette équation conduit à la relation ci-après donnant la distance parcourue au bout d'un temps t

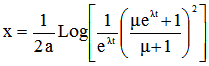équation [5]

En éliminant le temps entre les équations [3] et [4], on peut obtenir la relation entre la distance parcourue x et la vitesse V:

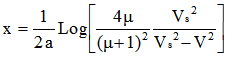équation [6]

Application

Le résultat important que l'on peut tirer des relations 4 et 6 est que le temps et la distance tendent vers l'infini lorsque la vitesse V se rapproche de la vitesse limite Vs. En conséquence, il n'est pas possible en toute rigueur d'atteindre la vitesse limite. Si l'on se satisfait d'atteindre 99% de la vitesse limite, le tableau 1 à double entrée nous donne la distance à parcourir pour atteindre cette valeur de la vitesse en fonction de la vitesse initiale en haut de la descente et de la pente.

On voit qu'il doit toujours dépasser 500 m pour se rapprocher de cette vitesse.

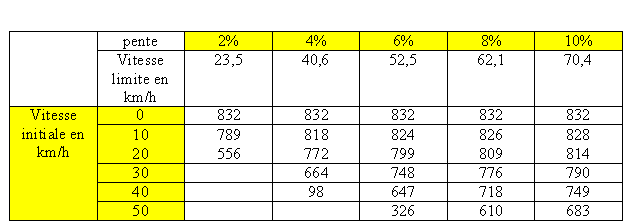
Tableau 1. Distance nécessaire en mètres pour atteindre la vitesse limite.

Sur la figure 1, pour une pente à 2%, on a tracé les courbes représentant l'évolution de la vitesse en fonction de la distance et cela pour 3 valeurs de la vitesse initiale.

Sur la figure 2, la pente est passée à 6%.

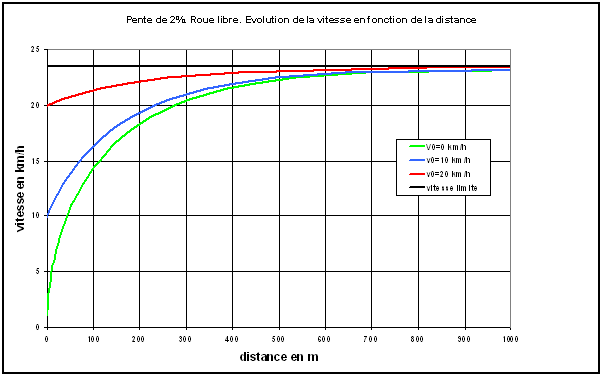
Fig.1. Descente en roue libre : évolution de la vitesse pour une faible pente

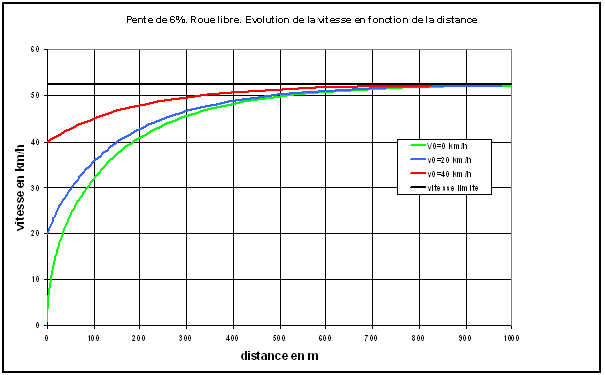
Fig.2. Descente en roue libre : évolution de la vitesse pour une pente à 6%

Une autre question que l'on peut se poser est la suivante : lorsque l'on roule en groupe et qu'arrive une descente, le groupe a vite fait de se disloquer : les uns vont plus vite que les autres. Quelle en est l'explication ?

La vitesse limite dépend du rapport W/Cx W et Cx sont des paramètres qui caractérisent chaque cycliste. Plus ce rapport sera élevé, plus importante sera la vitesse limite. Si l'on prend un gros gabarit, ce rapport augmente avec le poids du cycliste, le poids est donc un élément favorable pour aller vite en descente. Mais plus le gabarit du cycliste est imposant, plus le coefficient de pénétration dans l'air Cx augmente, ce qui fait diminuer le rapport W/Cx, l'augmentation de Cx est donc un élément défavorable. W et Cx ont donc des effets qui se contrarient.

Pour voir quel est le facteur qui l'emporte, il faudrait connaître la variation de Cx en fonction du poids. On peut faire l'estimation grossière suivante :

En éliminant H, on obtient :

Cx=k W^2/3

Ce qui entraîne :

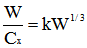
Le rapport est donc proportionnel à la racine cubique du poids, c'est le poids qui l'emporte finalement. Les gros gabarits seraient donc favorisés dans les descentes. L'écart n'est pas à négliger.

Pour fixer les idées prenons une pente à 6%, un cycliste de 60 kg caractérisé par Cx=0.20 et un second cycliste de 90 kg dont le Cx devrait être de 0.23.

La vitesse limite du petit gabarit sera de 44,1 km/h et celle du gros gabarit de : 50,3 km/h.

Si le groupe roule tranquillement à 20 km/h avant la descente, à partir des équations ci-dessus, on peut calculer qu'au bout de 30 secondes de descente en roue libre le gros gabarit aura parcouru 308 m et le petit gabarit seulement 280 m, soit un écart de 28 m.

Chaque cycliste ayant un poids et un coefficient de pénétration dans l'air différent, il n'est pas étonnant que le peloton s'étire dans la descente.

Descendre en pédalant

Comme on le verra plus tard, la vitesse atteinte dans une descente en roue libre n'est certainement pas suffisante pour aborder la cote avec suffisamment d'élan pour pouvoir gravir toute la cote sans pédaler. Pour accroître cette vitesse, on peut donc songer à pédaler. Ira-t-on vraiment plus vite ?

Comme en roue libre, le cycliste va prendre de la vitesse, la résistance de l'air va croître et atteindre finalement la valeur de la somme des forces qui attirent le cycliste vers le bas. La seule différence est que le cycliste fournit une force motrice qui va s'ajouter à la force de pesanteur. La vitesse va aussi se stabiliser à une valeur Vs.

En pédalant, le cycliste fournira une puissance P que l'on suppose constante lorsque la vitesse sera stabilisée.

Cette vitesse est solution de l'équation [1] où P n'est pas nul et qui est une équation du 3ème degré en V. Elle n'a pas de solution analytique.

Pour résoudre cette équation, il faut utiliser une méthode de résolution numérique.

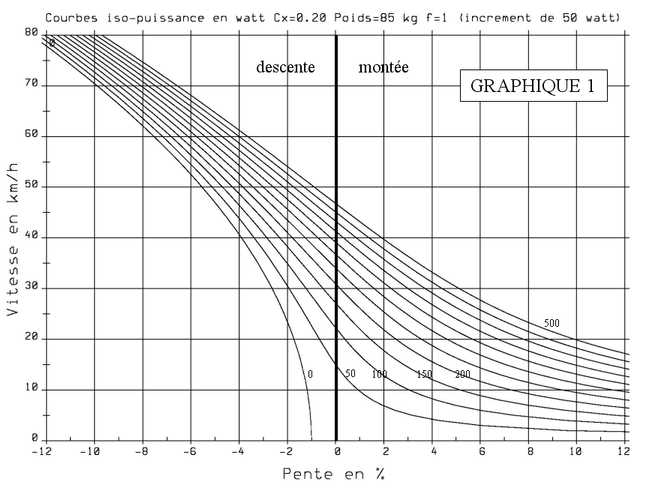
Fig.3. Vitesse limite en fonction de la pente et de la puissance fournie

La figure 3 tirée du document « Le vélo en équation » montre clairement la vitesse que l'on peut atteindre en descente pour différentes valeurs de la pente et pour des puissances fournies différentes. Ainsi, en lisant le graphique, on voit que pour une pente à 6%, un cycliste en roue libre (P=0) atteindra 52 km/h. En fournissant une puissance de 150 watt, il atteindra une vitesse de 58 km/h et avec une puissance de 500 watts digne d'un sprinter professionnel il atteindra seulement 68 km/h.

Une constatation s'impose donc: en pédalant, il est difficile d'accroître très nettement la vitesse, c'est la valeur de la pente qui permettra d'aller vraiment plus vite. Nous en tirons donc la conclusion qu'il vaut mieux ne pas pédaler, en profiter pour se reposer et réserver ses forces pour la remontée si nous ne sommes pas un coureur professionnel en compétition.

Comme en roue libre, il faut cependant un certain temps pour atteindre ou tout au moins s'approcher de la vitesse limite. On peut remettre cela en équation mais puisque nous avons décidé de ne pas pédaler, nous n'aborderons pas le problème. Cette question du temps nécessaire pour se stabiliser sera abordée en détail pour la montée qui est plus préoccupante que la descente.

Monter une côte sans pédaler

Après la descente, c'est maintenant la punition : il faut monter mais le premier réflexe est de retarder le plus possible l'instant où l'on devra pédaler.

Prenons un cycliste qui a donné toute son énergie pour prendre de la vitesse dans la descente. Il se présente à vive allure au bas de la montée et cesse alors de pédaler. D'un point de vue mécanique, le cycliste a emmagasiné de l'énergie dans la descente que l'on appelle de l'énergie cinétique. Cette énergie va lui permettre d'effectuer certainement une partie de la montée mais pourra-t-il aller jusqu'au sommet de la cote ?

Résolution

Reprenons l'équation du mouvement appliquée à l'ensemble cycliste et vélo :

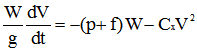équation [2]

On notera que cette équation ne prend pas en compte l'énergie cinétique de rotation des roues que nous estimons négligeable par rapport à l'énergie cinétique de translation. On rappellera en effet que l'énergie emmagasinée par un corps de masse M qui se déplace à une vitesse V comprend l'énergie cinétique de translation due au déplacement du corps et l'énergie cinétique de rotation si le corps ou une partie du corps est soumis à une rotation, ce qui est le cas des roues d'un vélo ainsi que diverses autres pièces : plateau, manivelle, etc. L'énergie cinétique de translation est égale à :

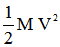
et l'énergie cinétique de rotation à :

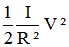
I est le moment d'inertie des pièces en rotation R est le rayon des roues.

Pour comparer la valeur de ces deux types d'énergie, il suffit de comparer les termes M et I/R² (ces deux quantités s'expriment en kg).

La valeur de I/R² pour un vélo de route est compris entre 1 et 1,2 kg. On la négligera donc vis-à-vis de la masse cycliste + vélo d'autant plus que cette masse varie selon que le cycliste est à jeun ou a bien bu et bien mangé.

On posera :

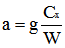
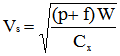
Avec ces notations, l'équation devient :

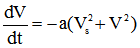
Soit :

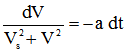
Compte tenu qu'à l'instant t=0, on a V=V0 l'intégration de cette équation différentielle aboutit à :

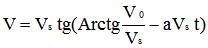équation [8]

La distance parcourue x en fonction du temps est solution de l'équation différentielle :

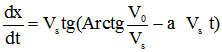équation [9]

Compte tenu qu'à l'instant t=0 on a : x=0 , la solution de cette équation est :

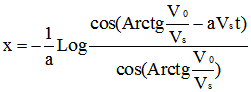équation [10]

La vitesse V s'annulera au bout d'un temps tmax donné par :

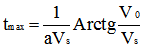
En remplaçant a et Vs par leur expression et en exprimant la distance en mètre, la distance parcourue xmax au moment où le cycliste devra reprendre le pédalage sera égale à :

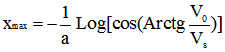équation [11]

Applications

Pour utiliser cette forule, il est nécessaire d'être expert dans le fonctionnement d'une calculette assez sophistiquée comportant les fonctions trigonométriques et la fonction logarithme.

Nous présentons sur la figure 4 les résultats obtenus pour un cycliste pesant 85 kg avec son vélo, caractérisé par un coefficient de pénétration dans l'air de 0.20 et roulant sur une chaussée dont le coefficient de frottement est de 1%. Les graphiques donnent la distance maximale atteinte exprimée en mètres pour différentes pentes de la côte comprises entre 2 et 10% et pour des vitesses initiales comprises entre 20 et 60 km/h. Les flèches indiquent la distance à laquelle le cycliste s'arrêtera, pour différentes valeurs de la vitesse initiale.

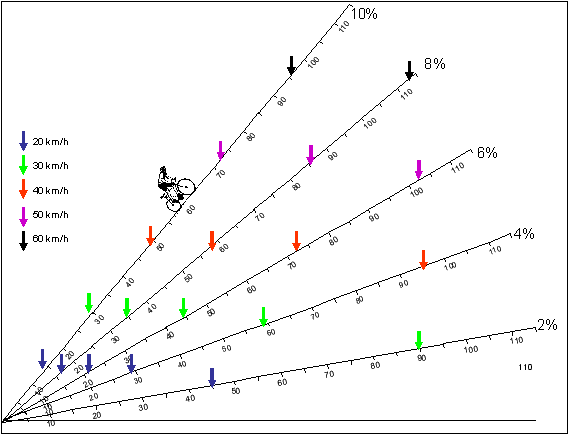
Fig.4. Distance limite atteinte en montée sans pédaler

On constate que dès que la pente atteint 4%, la vitesse initiale dans le creux doit être importante si la longueur de la côte est de 100 m.

Il ne faut donc pas rêver : il faudra pédaler pour sortir du creux.

La courbe « en roue libre » de la figure 5 montre la façon dont la vitesse décroit. Ce qui est caractéristique, c'est qu'au début la vitesse décroît de façon assez régulière puis qu'à partir d'une certaine distance (80 m dans l'exemple donné) elle chute rapidement avant de tomber à zéro. Dans cet exemple, le cycliste s'arrêtera au bout de 105 m et devra donc reprendre le pédalage si la cote est plus longue.

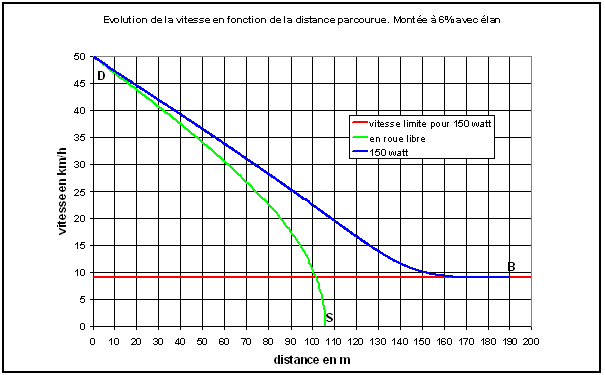
Fig.5. Evolution de la vitesse en montée

Pédaler pour passer la bosse

Comme on vient de le constater, il est vraiment peu probable que l'on puisse prendre suffisamment d'élan pour passer la bosse sans pédaler. On peut donc se poser les questions suivantes :

jusqu'à quelle distance, le fait d'avoir pris de l'élan se fera sentir ?
faut-il mieux pédaler dès le bas de la cote ou attendre un peu?

Résolution

Pédaler, c'est fournir une force motrice Fm. On va supposer que le cycliste fournit cette force motrice dès le bas de la côte.

L'équation du mouvement [2] devient :

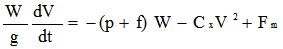équation [12]

On posera :

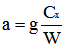
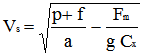
L'équation du mouvement s'écrit alors plus simplement :

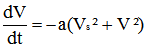
Le cycliste a mille et une façons d'exercer une force motrice Fm, car il est libre de pédaler comme il veut. Nous forulerons à priori deux hypothèses :

le cycliste exerce une force motrice constante
le cycliste fournit une puissance constante

mais nous allons montrer d'abord que la première hypothèse n'est pas réaliste.
En effet, dans le premier cas, où la force Fm reste constante, la puissance varie car la force motrice Fm est liée à la puissance P par la relation :

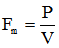équation [13]

On voit sur cette relation que lorsque la vitesse V va diminuer, la puissance P va également diminuer puisque Fm doit rester constant. Le cycliste fournit donc un effort irrégulier. Pour estimer la valeur de cette force motrice, il est logique de dire qu'elle sera égale à la force motrice qu'il développera lorsque l'influence de l'énergie cinétique qu'il avait acquise au bas de la cote ne se fera plus sentir et qu'il sera alors en régime de « croisière ». Si dans ce régime de croisière, il développe une puissance P, la force motrice correspondant à cette puissance P est donnée par l'équation [13]. Si l'on fait une application numérique, en prenant, par exemple P=150 watt, ce qui est modeste, la vitesse de croisière sera égale à 8,9 km/h pour une cote à 6% (voir figure 3), d'où :

Fm=6,07 kg

Si cette force est supposée constante depuis le début de la montée, en abordant la cote à une vitesse de 40 km/h, l'équation [13] nous dit que la puissance développée dès l'amorce de la montée est égale à 674 watt. Une telle valeur de la puissance n'est pas réaliste.

En conclusion, l'hypothèse d'un pédalage à force motrice constante est à exclure.

Dans le second cas, la force motrice Fm va augmenter lorsque la vitesse diminuera mais, la puissance fournie restant constante, l'effort sera donc régulier, la fréquence cardiaque du cycliste devrait rester stable.

Fournir une puissance constante est un mode de pédalage beaucoup plus proche de la réalité. Nous allons donc traiter ce dernier cas.

En exprimant Fm en fonction de la puissance, la valeur de Vs devient :

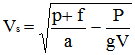
et l'équation différentielle du mouvement se complique un peu:

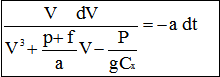équation [14]

Cette équation n'a hélas pas de solution analytique mais on peut la résoudre cas par cas par une méthode numérique : c'est ce qui sera fait dans l'application qui suit.

Application

Reprenons notre cycliste qui se présente au bas de la cote à 6% avec une vitesse de 50 km/h. Il décide de pédaler et de fournir immédiatement sa puissance habituelle de 150 watt. Sa vitesse va progressivement diminuer et se stabiliser à la vitesse de croisière de 8,9 km/h fournie par la figure 3.

Pour avoir l'évolution de la vitesse ainsi que le temps et la distance à partir desquels il atteindra cette vitesse de croisière, il faut intégrer l'équation [14].

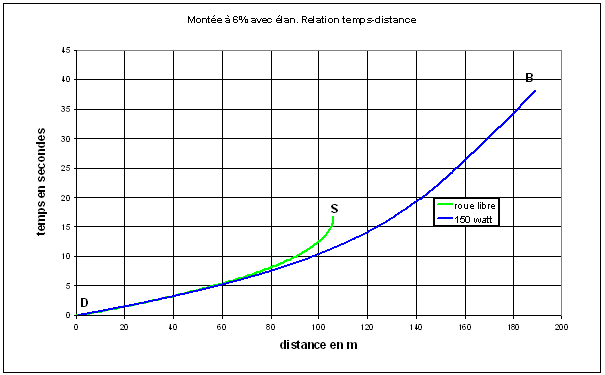
Fig.6. Relation temps-distance en montée avec élan

Comme il vient d'être dit, il n'est pas possible de donner une formule générale qui soit solution de cette équation. En revanche, en donnant une valeur aux paramètres intervenant dans cette équation, on peut la résoudre par une méthode dite numérique. On a donc fixé à 85 kg le poids du cycliste et de son vélo, à 50 km/h la vitesse initiale au bas de la cote, à 6% la pente, et à 150 watt la puissance fournie par le cycliste.

Le résultat de l'intégration numérique est présenté sur les figures suivantes :

figure 5. La courbe « 150 watt » montre la décroissance de la vitesse. Bien sûr, puisque l'on pédale, cette décroissance est moins importante qu'en roue libre, elle est très régulière. La vitesse de croisière est atteinte au bout d'une distance de 185 m environ (point B).
figure 6. La courbe « 150 watt » donne le temps écoulé en fonction de la distance. La vitesse de croisière est atteinte au bout de 37 secondes.

Le bilan : quelle stratégie adopter pour franchir la bosse ?

'

Comparons trois stratégies que notre cyclo de 85 kg tout compris peut mettre en œuvre pour atteindre le point A en un temps identique. Ces stratégies sont illustrées sur la figure 7.

Comparons maintenant les énergies fournies dans ces trois stratégies :

Première stratégie : puissance de 150 watt fournie durant 42.48 secondes soit une dépense énergétique de 150 x 42.48= 6372 joules
Seconde stratégie : une puissance de 206 watt fournie durant 30.48 secondes soit une dépense énergétique de 206 x 30.48 = 6278 joules
Troisième stratégie : une puissance de 260 watt fournie durant 25.78 secondes soit une dépense énergétique de 260 x 25.78 = 6703 joules

C'est donc la seconde stratégie qui l'emporte avec une économie d'énergie d'environ 1.5% par rapport à la première stratégie mais cette différence est peut-être de l'ordre de grandeur de la précision du calcul par « intégration numérique ». Bien sûr, il faut pour cela être apte à fournir une puissance plus forte durant un laps de temps plus court : si l'on ne peut pas fournir un effort supérieur à 150 watt, la question ne se pose pas. Quant à la troisième stratégie, elle est plus énergivore, on s'en doutait un peu, et demande une forte puissance lors du redémarrage pour rattraper le temps perdu.

La conclusion finale est donc qu'il vaut mieux profiter d'abord de son élan pour se reposer puis reprendre le pédalage en cours de montée ni trop tôt ni trop tard, quitte à fournir un effort supérieur à son effort habituel.

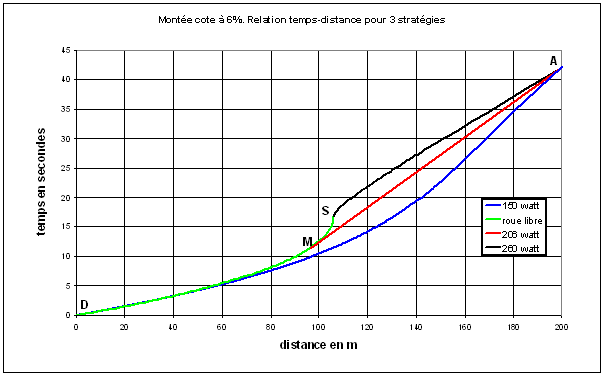
Figure 7. Trois stratégies pour monter la cote

Auteur: Jacques Fine
contact@velomath.fr

Haut de page

Retour accueil