Vitesse et puissance lors d'un sprint

Mai 2016
contact@velomath.fr

Le sprint est certes une action qui n'intéresse pas beaucoup le cyclotouriste ou le promeneur mais c'est une action qui est la raison de vivre de nombre de coureurs cyclistes afin de franchir la ligne quelques centimètres devant le concurrent.
Sprinter, c'est fournir l'effort le plus grand possible, effort qui ne peut être soutenu que durant un laps de temps assez court. Notre propos est d'établir les relations entre cet effort et la vitesse atteinte par le coureur, la distance qu'il parcourra et le temps qu'il mettra et d'essayer ensuite d'en tirer des conclusions pratiques.

L'équation du mouvement

Les forces à prendre en compte sont explicitées dans le document « le vélo en équation » auquel on pourra se reporter. Cependant, dans le présent document, on utilisera les unités légales du système international et non pas les unités familières aux cyclistes et cela afin de ne pas alourdir l'écriture des relations.
Adoptons donc les notations suivantes:

Sprinter, c'est fournir brutalement une force motrice F_m qui s'exprime en Newton. Le problème a été abordé dans le document écrit antérieurement : « Des creux et des bosses » où l'on cherchait à évaluer l'effort à fournir par un cycliste pour gravir une côte.
La force motrice est comparable à la force que pourrait exercer une personne qui pousserait le cycliste ou bien à la tension de la corde entre le cycliste et un véhicule qui le tracterait. Il faut bien noter que cette force F_m ne doit pas être confondue avec la force que le cycliste exerce directement sur les pédales. La force F_m est induite bien sûr par le pédalage du cycliste et il y a une relation entre les deux que nous allons établir. Avec les notations suivantes;

on a la relation:

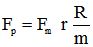
Si l'on désire avoir des ordres de grandeur des forces F_m et F_p, on peut s'aider du calculateur proposé ici.
Par ailleurs, le mouvement de pédalage est analysé et modélisé dans le document « Le mouvement de pédalage ».
Avec les unités adoptées, l'équation fondamentale de la dynamique F=Mγ appliquée à l'ensemble cycliste et vélo s'écrit :

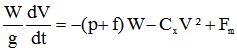équation [1]

Remarque. Le cycliste et le vélo sont animés d'un mouvement de translation mais les roues sont en plus animées d'un mouvement de rotation, ce qui n'est pas pris en compte dans l'équation [1] où il faudrait remplacer la masse M (soit W/g) par : 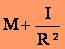I étant le moment d'inertie des roues et R leur rayon et donc modifier le premier membre de l'équation [1]. Une façon d'opérer est de modifier la valeur de g en remplaçant g par g' tel que : 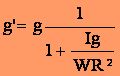Pour les roues légères des routards, la valeur de I/R² est de l'ordre de 500 à 600 grammes par roue. Pour un poids vélo+cycliste de 800 N, il faudrait donc prendre g'=9.67 m/s²

On posera :

L'équation [1] s'écrit alors :

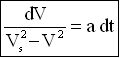équation [2]

L'intégration de cette équation différentielle va nous donner la vitesse du cycliste en fonction du temps. Le problème mathématique, c'est que le terme Vs dépend de la force F_m que le cycliste fournit et cette force F_m peut ne pas être constante tout au long du sprint. Si la force F_m est constante, l'équation s'intègre sans difficultés, sinon, il faut la résoudre par une méthode numérique. Il faut donc connaître la façon dont le cycliste exerce son effort et il y a une infinité de façon pour exercer cet effort. Cela ne dépend donc que du cycliste. Cependant, on peut formuler deux hypothèses simples:

Sprint à force constante

Cette façon de sprinter revient à fournir une très forte puissance au démarrage du sprint puis à la diminuer progressivement. La force F_m étant supposée constante, l'intégration de l'équation [2] aboutit aux relations ci-dessous.

Relation donnant le temps en fonction de la vitesse :

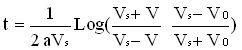équation [3]

V0 est la vitesse à l'instant t=0

Relation donnant la vitesse en fonction du temps

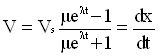équation [4]

après avoir posé :

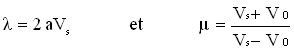
Relation donnant la distance parcourue en fonction du temps

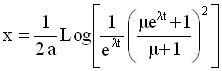équation [5]

Relation donnant la distance parcourue x en fonction de la vitesse V:

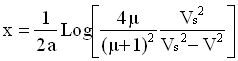équation [6]

Pour appliquer ces équations, un calculateur vous est proposé.

Application numérique 1.

Caractérisons le cycliste par : W=800 N (poids du cycliste et du vélo) et Cx=0.20
Caractérisons la route par : p=0 et f=0.01
Supposons que le cycliste roulait à 42 km/h. En roulant à 42 km/h, il fournissait une puissance P de 411 watts que l'on calcule par la relation (voir « Le vélo en équation ») :

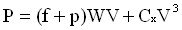
La force motrice correspondante est donnée par F_m=P/V soit F_m= 35.22 N
A l'instant t=0, il lance son sprint en fournissant une force motrice que l'on va fixer à 100 N.
Sa vitesse va croître et va tendre asymptotiquement vers Vs, soit 77 km/h.
La figure 1 donne l'évolution de la vitesse ainsi que la distance parcourue calculées à partir des équations [4] et [5] durant les 30 premières secondes.

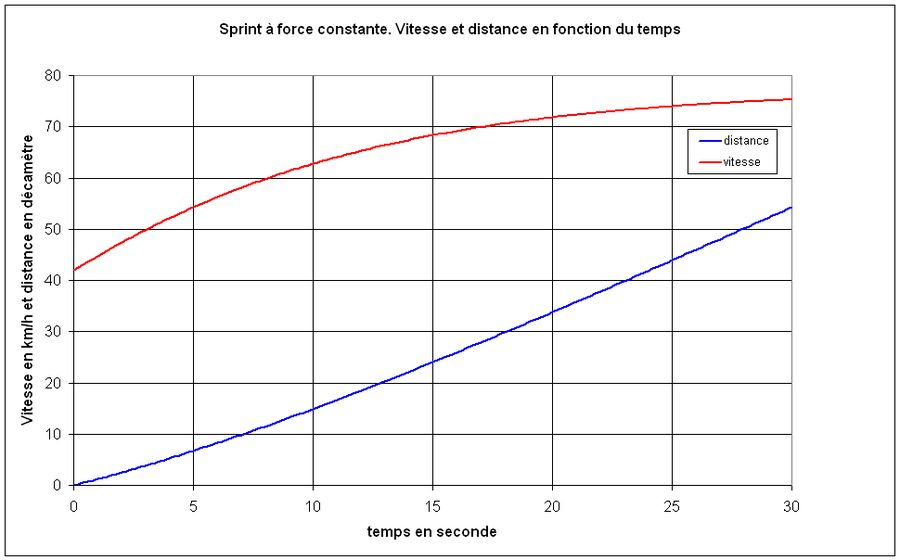
Fig.1. Vitesse et distance pour un sprint à force constante

En fournissant une force constante F_m, le cycliste fournit une puissance P variable, celle-ci étant égale à F_m V. La puissance est proportionnelle à la vitesse.
La courbe de la figure 2 donne l'évolution de la puissance en fonction du temps.

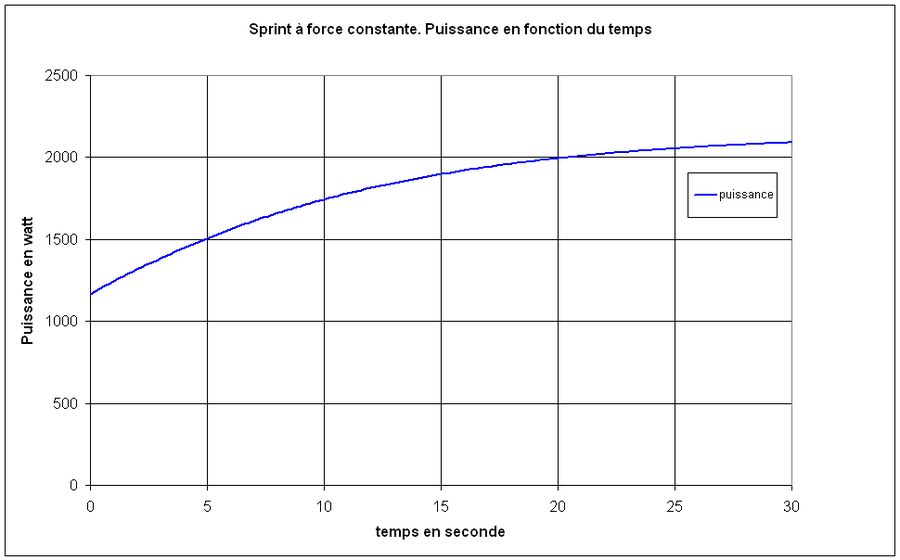
Fig.2. Puissance pour un sprint à force constante

Il va de soi que le cycliste ne peut pas fournir cet effort durant 30 secondes et ne peut pas atteindre la vitesse limite, car il sera épuisé bien avant. Pour prendre en compte la capacité du cycliste à fournir un effort intense, nous admettrons que ce dernier est épuisé lorsqu'il atteint une certaine vitesse. Par exemple, nous dirons que le cycliste ne peut pas dépasser 60 km/h et dès qu'il atteint cette vitesse, il ne pédale plus et se met en roue libre. Dans cette application, il atteint 60 km/h au bout de 8.14 secondes.

Il est intéressant de suivre le mouvement du cycliste après l'arrêt du pédalage car, si le sprint a été lancé trop tôt, le coureur n'aura pas encore franchi la ligne d'arrivée au bout de 8.14 secondes.
Le mouvement du cycliste en roue libre est régi par les mêmes équations établies que précédemment, il suffit de prendre la force d'accélération F_m égale à zéro.
La figure 3 reprend donc la figure 1 en donnant l'évolution durant 12 secondes de la vitesse et de la distance parcourue en tenant compte de la limitation de l'effort du coureur.

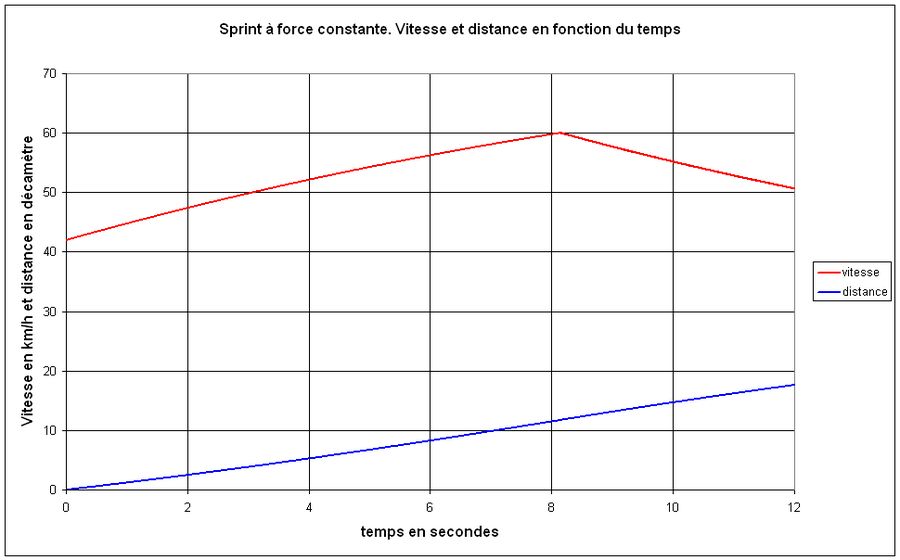
Fig.3. Vitesse et distance en limitant la vitesse à 60 km/h

Application 2. Comparaison de deux cyclistes non identiques.

Provoquons un sprint entre deux coureurs dont les aptitudes sont caractérisées par la même vitesse maximale atteinte, soit 60 km/h mais qui diffèrent un peu sur la manière d'atteindre cette vitesse. Le premier fournit une force d'accélération de 100 N et le second une force plus forte de 120 N. Lequel des deux coureurs gagnera le sprint ?
Sur la figure 3, on a déjà calculé la courbe donnant la distance parcourue en fonction du temps pour le premier coureur développant 100 N.
Il suffit de refaire le même calcul pour le second coureur et de présenter les courbes sur le même graphique, ce qui est fait dans la figure 4.
On constate que c'est le coureur 2 qui est devant tant que la distance reste inférieure à 147 m. Au-delà de cette distance, qui est atteinte au bout de 9.98 s, c'est le coureur 1 qui passe en tête.
On en conclu donc que la longueur du sprint est un facteur important. Un coureur développant une forte puissance au départ peut ne pas gagner si le sprint est lancé très tôt.

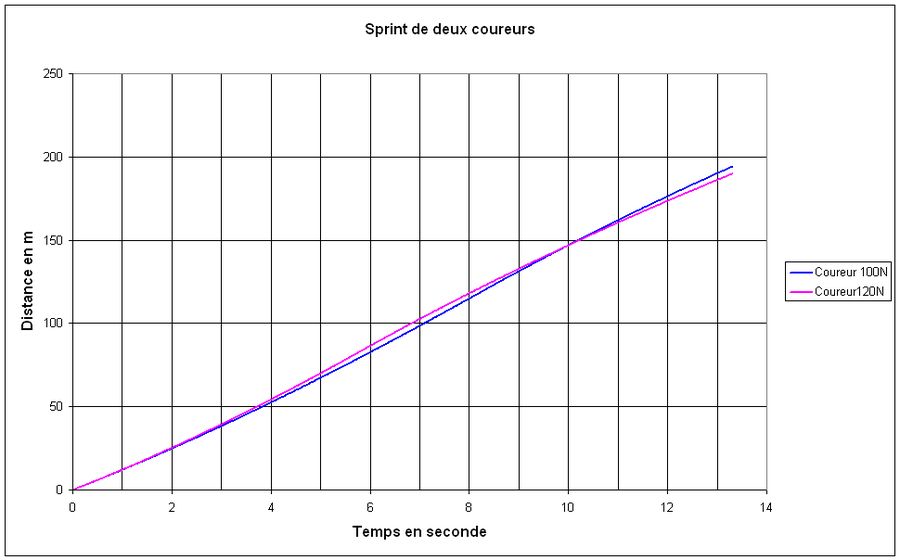
Fig.4. Sprint de deux coureurs

Application 3. Comparaison de deux cyclistes identiques

Maintenant, faisons sprinter deux coureurs possédant strictement les mêmes caractéristiques. Ils seront forcément ex aequo s'ils lancent le sprint au même instant, au centième de seconde près. Supposons que le premier coureur lance le sprint et que le second coureur réagisse une seconde après. Lequel des deux coureurs va l'emporter ?
Sur le graphique de la figure 5, on a représenté en fonction du temps la distance qui va séparer le coureur 1 du coureur 2. On constate que le coureur 1 va prendre de l'avance qui va atteindre presque 5 m au bout d'environ 9 secondes (après avoir parcouru 118 m) mais au-delà l'écart va diminuer et le coureur 2 passera devant au bout de 17 secondes environ soit après 243 m.
La distance à laquelle le sprint est lancé a donc une importance primordiale.

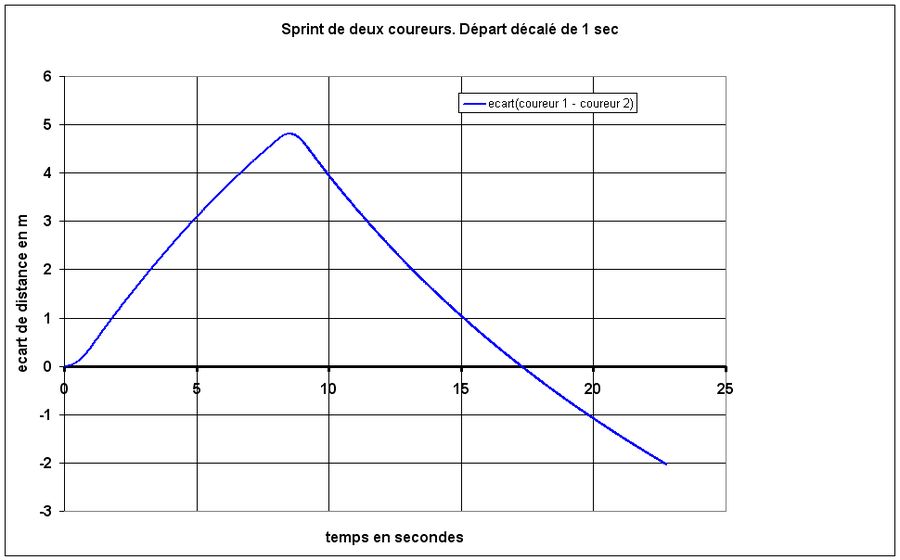
Fig.5. Sprint de deux coureurs à caractéristiques identiques

Sprint à puissance constante

Cette façon de sprinter revient à exercer une très grande force sur les pédales au démarrage du sprint puis à la relacher progressivement. La force motrice peut être comparée à celle fournie par une personne qui veut lancer un coureur après un arrêt: cette poussée est très forte au début puis diminue au fur et à mesure que le coureur prend de la vitesse.

Avec cette hypothèse, la force d'accélération F_m (qui est égale à P/V) est inversement proportionnelle à la vitesse et donc dépend du temps. Le paramètre Vs où figure la variable F_m dépend donc du temps. L'équation différentielle [2] à résoudre n'a pas de solution analytique et par conséquent on ne peut pas établir des relations donnant vitesse, distance en fonction du temps. L'équation doit être résolue par une méthode numérique, cas par cas.
Le calculateur proposé permet cette résolution.
La comparaison des résultats obtenus dans les deux hypothèses : force constante ou puissance constante doit être faite sur des applications numériques. C'est ce qui a été fait en reprenant les données précédentes.
On obtient le graphique 5, relatif au coureur qui fournissait une force A=100 N, donnant la vitesse en fonction du temps, graphique analogue au graphique 3 et où l'on a aussi limité la vitesse à 60 km/h. La puissance que l'on a attribuée est la puissance moyenne fournie dans l'application du graphique 2 dans l'intervalle de vitesse 42-60 km/h, soit 1440.7 watts.
Sur le graphique 6, on a reproduit en pointillé les courbes du graphique 3 afin de visualiser la comparaison. Les résultats sont évidemment très proches les uns des autres.

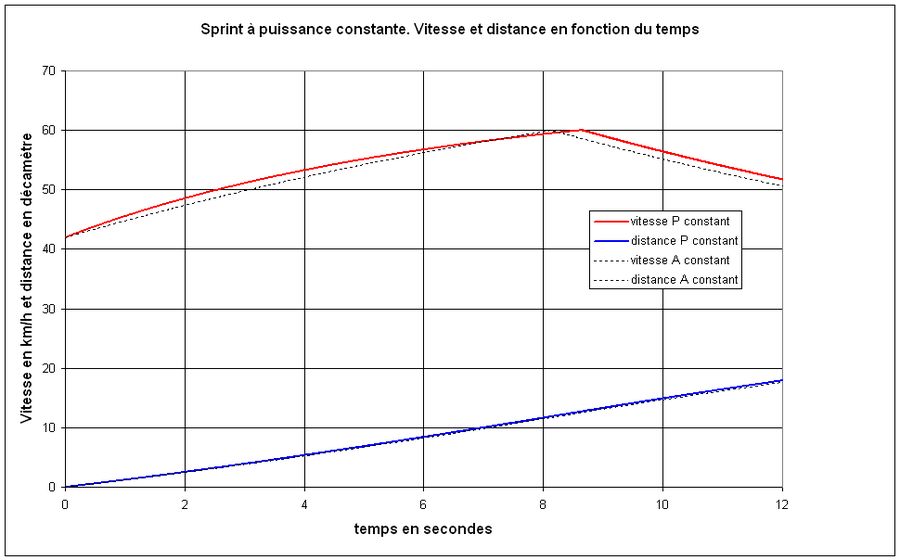
Fig.6. Vitesse et distance en limitant la vitesse à 60 km/h

Quelle hypothèse retenir ?

Les deux hypothèses ne donnent pas des résultats très différents. Il est probable que dans la réalité le coureur travaille à la fois à force variable et à puissance variable également. Pour trancher, il suffit d'enregistrer la puissance au moyen d'un capteur de puissance embarqué. Faute de disposer de tels outils, nous n'avons pas trouvé des enregistrements de sprint en navigant sur Internet.

Conclusions

Quelle que soit l'hypothèse adoptée pour quantifier l'effort du cycliste lors d'un sprint, les calculs mettent en évidence que le coureur le plus « fort » ne gagnera pas forcément le sprint. La stratégie est tout aussi importante que la force. Savoir à quel moment lancer le sprint nécessite de connaître les caractéristiques de ses adversaires, ce n'est pas très simple.

Haut de page

Accès au calculateur

Retour accueil