Rouler en accordéon

En roulant en groupe avec mon club de cyclo-touristes, il est arrivé maintes fois que le groupe ou une partie du groupe accélère sans raisons apparentes, puis au bout d'un moment ralentisse, voyant que tout le monde n'a pas suivi ou que certains peinent. Cette pratique est peut-être plus ludique qu'une randonnée effectuée au métronome mais personnellement cela ne me convient pas, préférant utiliser l'énergie dépensée de cette façon pour aller plus loin car ce mode de comportement est consommateur d'énergie comme ce document va le démontrer.

Soit un cycliste A parcourant la distance d, à la vitesse constante V₀. Il mettra donc un temps t₀ égal à t₀=d/V₀Pour ce faire, il devra fournir une force motrice F (en newton) donnée par la relation (Voir « le vélo en équation ») :

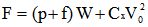équation [1]

où:

et l'énergie E₀ qu'il devra dépenser sera :

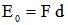équation [2]

Prenons un deuxième cycliste B qui effectuera le même parcours dans le même temps t₀ mais qui ne voudra pas rouler à la même vitesse durant tout le parcours.
Il fera une distance d₁ à la vitesse V₁ et le reste du parcours, soit d₂= d-d₁, à la vitesse V2.
Comme il est sensé mettre le même temps que le cycliste A, la vitesse V₂ et la vitesse V₁ sont liées.
Le temps mis pour parcourir la distance d₁ est égale à : t₁=d₁/V₁
Le temps mis pour parcourir la distance d₂ est égale à : t₂=d₂/V₂
On aura donc la relation :

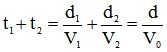
Si le cycliste parcourt la distance d₁ à la vitesse V₁, il parcourra alors le reste du parcours d₂=d-d₁ à la vitesse V₂ donnée par :

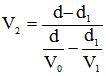
Pour effectuer le parcours, il fournira une force motrice F₁ pour rouler à la vitesse V₁ et une force F₂ pour rouler à la vitesse V₂. Ces forces sont données par les relations suivantes :

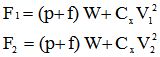
L'énergie totale à fournir est donc :

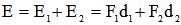
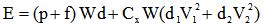équation [3]

Existe-t-il une paire de valeur V₁, V₂ pour laquelle l'énergie E est minimum ?

Pour cela, il faut trouver le minimum de la fonction :     d₁ V₁² + d₂ V₂²
sachant que les variables d₁, d₂ et V₁, V₂ sont liées par les relations :

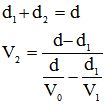
On peut démontrer que le minimum correspond à :V₁=V₀     et    d₁=d      d₂=0
Une démonstration de ce problème de minimum est présentée de façon plus générale dans le document: "Gestion optimale d'un parcours cycliste".

On en tire donc la conclusion que la dépense minimale d'énergie sera obtenue lorsque le parcours sera effectué à vitesse constante.

Application

Effectuons un parcours de 100 km à la vitesse de 25 km/h. Nous mettrons 4 heures.
Adoptons d'autres allures tout en effectuant le parcours en 4 heures : commençons par parcourir une distance d₁ à la vitesse V₁.
Le tableau 1 à double entrée donne la vitesse V₂ à respecter dans la seconde partie du parcours.
Sur la première ligne, on trouvera la vitesse V₁ allant de 30 à 50 km/h
Dans la première colonne, on trouvera la distance d₁ durant laquelle on a roulé à la vitesse V₁.

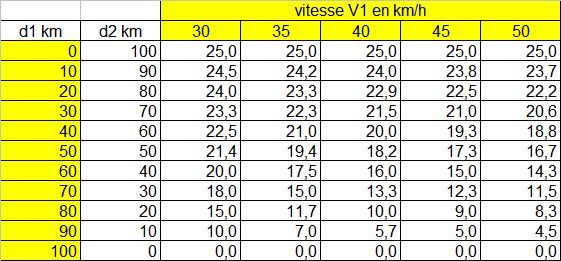
Tableau 1. Relation entre la vitesse V₁ et la vitesse V2

Ainsi, si l'on roule durant 20 km à 35 km/h, il faudra rouler à 23,3 km/h durant la seconde partie du parcours.
L'important, c'est de comparer les énergies fournies dans ces différentes configurations.
Adoptons les valeurs suivantes pour caractériser le cycliste :

Avec ces paramètres, l'énergie fournie en effectuant le parcours à une vitesse constante de 25 km/h, exprimée en kilo-Joules, (relation [2]) est égale à : 1815 kJ
En parcourant 20 km à 35 km/h et 80 km à 23,3 km/h, l'énergie totale fournie sera de 1900 kJ, soit 5 % en plus.
Le tableau 2 donne en pourcentage par rapport au cas où le parcours est effectué à vitesse constante la dépense d'énergie supplémentaire dans les mêmes situations que celles du tableau 1.

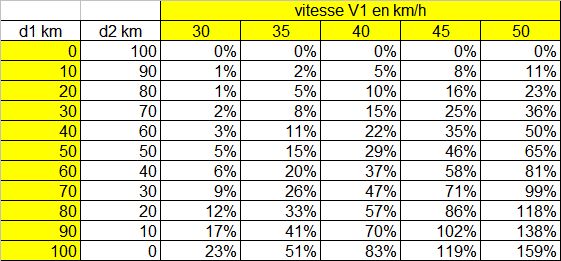
Tableau 2. Energie supplémentaire à fournir

On constate donc que, si l'on s'amuse tout au long du parcours à accélérer pour se détacher du peloton puis à ralentir pour l'attendre, la dépense énergétique sera plus importante. Personnellement, je préfère utiliser cette énergie pour aller plus loin

Jacques Fine. contact@velomath.fr
http://www.velomath.fr

Haut de page

Accueil du site