CALCULER LE COEFFICIENT DE PENETRATION DANS L'AIR
ET LE COEFFICIENT DE FROTTEMENT
PAR LE TEST DE DECELERATION
Il existe diverses méthodes expérimentales pour déterminer le coefficient de pénétration dans l’air Cx et le coefficient de frottement des pneus sur la chaussée désigné par f dans nos documents.
Le test dénommé « vitesse limite en descente » et proposé par ailleurs sur ce site permet de calculer le coefficient Cx. Ce test a l’inconvénient de nécessiter la connaissance de la valeur du coefficient de frottement f. En revanche, il est très facile à réaliser car il suffit de disposer sur son vélo d’un compteur ordinaire de vitesse et de lire sur ce compteur la vitesse limite atteinte en descente ; ainsi, on garde les deux mains sur le guidon et donc la position sur le vélo dont on veut juger de l’efficacité.
Le test dénommé « distance d'arrêt sur le plat », tel qu’il est proposé sur ce site, permet de déterminer le coefficient de frottement mais à condition de connaitre le coefficient Cx. Il est également simple à réaliser et ne nécessite pas de manipuler le compteur ou un chronomètre en roulant.
Si l'on ne connaît aucun des paramètres Cx ou f, on peut effectuer le test de "décélération" qui permet de déterminer à la fois le coefficient Cx et le coefficient f. Le protocole est le suivant :
- il faut choisir une route la plus plate possible comme terrain d’expérimentation et faire les tests un jour sans vent
- on roule à une vitesse assez élevée, puis on arrête le pédalage
- le principe est de noter le temps t1 mis pour passer d’une vitesse V1 plutôt élevée à une vitesse V2 assez proche de V1, mais cela ne suffit pas, il faut faire l’opération deux fois et mesurer le temps t2 mis pour passer d’une vitesse V3 plutôt lente à une vitesse V4. Par exemple, la vitesse V1 peut être de l’ordre de 40 km/h et V2 de 30 km/h tandis que la vitesse V3 sera plutôt de 10 ou 15 km/h.
- Ces deux mesures peuvent se faire au cours d’une même décélération ou bien en faisant deux essais totalement distincts, l’un après l’autre.
Si le test présente l’avantage de déterminer à la fois Cx et f, il présente l’inconvénient d’être plus difficile à réaliser à cause du chronométrage nécessaire. Il faut déclencher un chronomètre lorsque le compteur affiche une vitesse V1 que l’on mémorisera dans sa tête et le stopper à une vitesse V1 mémorisée elle-aussi. On peut donc être contraint de lâcher plus ou moins le guidon d’une main. Une solution est d’avoir un assistant sur le bord de la route qui manipulera le chronomètre aux tops que vous lui hurlerez. A bien noter que les vitesses V1 et V2 n’ont pas besoin d’être définies à l’avance mais peuvent être quelconques.
Théorie
Nous adopterons comme unités les unités utilisées par les cyclistes soit le poids en kg, la distance en km, le temps en heure et la vitesse en km/h. Bien que cela ait l’inconvénient d’alourdir les équations, cela a l’avantage de travailler avec des unités familières.
Adoptons les notations suivantes:
- W le poids cumulé du cycliste et du vélo en kg
- V la vitesse du cycliste en km/h
- p la pente de la route en %
- f le coefficient de frottement roues/chaussée
- Cx le coefficient de pénétration dans l’air
- l’unité de temps est l’heure
- l’accélération est exprimée en km/h²
- l’accélération de la pesanteur soit 9,81 m/s² a été arrondie à 10 (en conséquence 1 kg=10 Newtons)
|
Remarque très importante. En dynamique des fluides, la valeur de la résistance de l’air lorsque qu’un objet se déplace est de la forme : 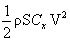
Or, d’une part ce qui nous intéresse est la valeur globale de : 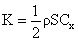
et d’autre part, c’est cette valeur globale que l’on peut mesurer avec des tests simples. C’est pourquoi, pour ne pas s’embarrasser des valeurs de ρ et de S dont la connaissance n’est pas indispensable, dans tous nos documents nous avons appelé Cx la valeur globale de K. |
L’équation du mouvement appliquée à l’ensemble cycliste et vélo :
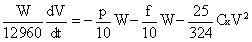 |
équation [1] |
On notera que cette équation ne prend pas en compte l’énergie cinétique de rotation des roues que nous estimons négligeable par rapport à l’énergie cinétique de translation. On rappellera en effet que l’énergie emmagasinée par un corps de masse M qui se déplace à une vitesse V comprend l’énergie cinétique de translation due au déplacement du corps et l’énergie cinétique de rotation si le corps ou une partie du corps est soumis à une rotation, ce qui est le cas des roues d’un vélo.
L’énergie cinétique de translation est égale à :
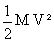
et l’énergie cinétique de rotation à :
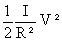
- I est le moment d’inertie des pièces en rotation
- R est le rayon des roues.
Pour comparer la valeur de ces deux types d’énergie, il suffit de comparer les termes M et I/R² (ces deux quantités s’expriment en kg).
La valeur de I/R² pour un vélo de route est compris entre 1 et 1,2 kg. On la négligera donc vis-à-vis de la masse cycliste + vélo d’autant plus que cette masse varie selon que le cycliste est à jeun ou a bien bu et bien mangé.
On posera :
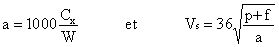
Dans notre test, la valeur de p est nulle puisque nous avons choisi une route plate, mais il est toujours possible de tenir compte d’une légère pente si celle-ci est connue et si elle est positive (montée).
Avec ces notations, l’équation devient :
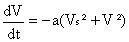 |
équation [2] |
Soit :
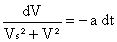
Compte tenu qu’à l’instant t=0, on a V=V0 l’intégration de cette équation différentielle aboutit à :
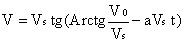 |
équation [3] |
Appliquons à notre test. En prenant t=0 au moment où l’on roule à la vitesse V1, on aura :
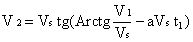
On a donc une équation où l’on a deux inconnues a et Vs. Pour résoudre le problème, il faut une seconde équation. Celle-ci sera obtenue en répétant le test pour deux vitesses V3 et V4, on aura ainsi cette seconde équation :
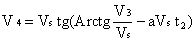
On dispose finalement d’un système de deux équations à deux inconnues, donc d’un système qui peut être résolu. La seule difficulté provient du fait que les deux équations ne sont pas des équations linéaires et que le système n’a pas de solution analytique. Il faut donc résoudre ce système par une méthode numérique, ce qui n’est pas un gros problème.
Cependant, pour éviter cette résolution numérique, on peut disposer d'une solution analytique approchée en procédant comme suit: on utilise l’équation [2] que l’on va appliquer à l’instant où la vitesse est égale à (V1+V2)/2, soit:
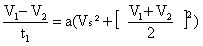
En remplaçant a et Vs par leur expression en fonction de f et Cx, on obtient la relation :
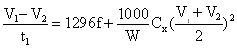 |
équation [4] |
et une relation tout à fait analogue avec V3, V4 et t2.
On dispose donc maintenant d’un système de deux équations linéaires en f et Cx que l’on peut résoudre sans difficultés.
Cette solution approchée est tout à fait satisfaisante.
|
Calculateur
Ne remplissez pas les cases jaunes, elles contiennent le résultat du calcul. |
| Haut de page | Retour accueil |