GESTION OPTIMALE D'UN PARCOURS CONTRE LA MONTRE
DEFINI PAR UNE TRACE GPX ET EN PRESENCE DE VENT
Le problème abordé ici est celui d'un cycliste disposant d'une certaine quantité d'énergie et voulant utiliser au mieux cette énergie pour effectuer un parcours défini par sa trace gpx. Utiliser au mieux, c'est aller le plus vite possible, autrement dit de rouler contre la montre. Ce problème a déjà été abordé dans le document "Gestion optimale d'un parcours cycliste" mais dans ce dernier document le parcours était défini par une succession de sections dont on connaît la longueur et la pente. Dans le présent document, on a ajouté l'existence du vent car tout cycliste connaît l'importance du vent. Le vent y est supposé de direction fixe et d'intensité constante mais son influence variera en fonction de l'orientation de la trajectoire du cycliste. Tout au long du parcours, vous pouvez avoir du vent de face, du vent latéral, du vent arrière
La théorie
La dépense d'énergie Ei faite pour parcourir un tronçon de longueur di est égale à:
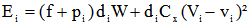
où:
- l'indice i est le numéro de la section qui varie de 1 à n, n étant le nombre total de section.
- pi est la pente de la section i et diest sa longueur
- f est le oopiefficient de résistance au roulement
- Cx le coefficient de pénétration dans l'air
- W le poids de l'ensemble cycliste et vélo.
L'énergie disponible E est la somme des énergies sur chaque tronçon soit
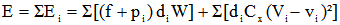
équation que nous pouvons aussi écrire:
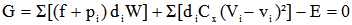
Si le cycliste roule à la vitesse Vi , le temps mis pour parcourir la section i sera égal à
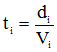
et le temps total T du parcours sera alors:
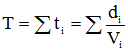
Optimiser le parcours consiste à chercher quelle sera la meilleure répartition des énergies Ei afin de minimiser le temps total T du parcours.
Le problème mathématique à résoudre est donc de minimiser la relation T sachant que les inconnues Vi sont liées par la relation G=0.
La résolution de ce problème peut se faire au moyen des multiplicateurs de Lagrange.
Pour cela, on posera:
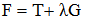
Le problème revient à minimiser la fonction F puisque G=0. Pour cela, on annulera les n dérivées partielles de la fonction F, ce qui s'écrit:
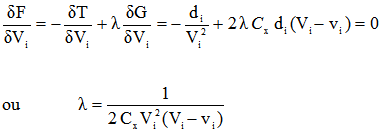
On dispose alors de n équations pour n+1 inconnues puisque λ est une inconnue. En ajoutant la relation G=0, on a finalement à résoudre un système d'équations de n+1 équations à n+1 inconnues. Ce système n'est pas un système linéaire mais un système de degré 3 en Vi. On ne peut pas le résoudre analytiquement, il faut passer par une résolution numérique.
Cependant, nous n'avons pas tenu compte d'une condition complémentaire sur la validité de la solution: il faut que la vitesse optimisée soit supérieure à la vitesse de stabilisation en roue libre dans une descente. En effet, en cas contraire, le cycliste devrait freiner pour ajuster sa vitesse à la vitesse optimisée, ce qui est évidemment une aberration car il irait plus vite sans freiner et sans la moindre dépense d'énergie. Dans l'algorithme d'optimisation, cela se traduit par une énergie Ei négative. Cet algorithme considère que l'énergie de freinage est restituée au cycliste et qu'il pourra l'utiliser sur d'autres sections, ce qui n'est malheureusement pas le cas d'un cycliste, même si certains peuvent penser que dans les descentes, on récupère. La condition à respecter est donc:
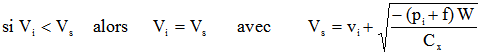
La solution mathématique est alors de fixer la vitesse à la valeur de stabilisation Vs en descente sur les sections où cette condition n'est pas respectée puis de recommencer le calcul de minimisation en éliminant ces sections en descente.
Le calculateur effectuera le cas échéant cette itération.
Calculateur
L'algorithme que nous avons choisi dans notre calculateur pour résoudre le problème de minimisation de la fonction F est le suivant. On peut remarquer que les inconnues V2 à Vn, en éliminant le paramètre λ, peuvent s'exprimer en fonction de V1 par la relation:
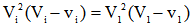
Il suffit alors d'incrémenter V1 en partant de 0, à chaque incrément de calculer les valeurs de V2 à Vn en résolvant des équations du troisième degré, de calculer avec ces valeurs la fonction G jusqu'au moment où l'on trouve un ensemble de valeurs V annulant la fonction G.
Utilisation du calculateur
Le calculateur s'applique à tout parcours défini par sa trace au format gpx.
Tout d'abord, en cliquant sur "parcourir", vous sélectionnerez sur votre ordinateur le fichier gpx du parcours à traiter puis vous l'exporterez sur Velomath en cliquant sur "Envoyer le fichier". Un message vous indiquera si l'opération a réussi.
A noter: il se peut que vous soyez seulement intéressé par un simple Aller-Retour en ligne droite et non pas par un parcours réel plus complexe. Dans ce cas, téléchargez et utilisez le fichier AR.gpx qui est une ligne droite orientée du Nord vers le Sud, sur du plat. On peut démontrer en reprenant la théorie ci-dessus que la répartition optimale de l'énergie entre l'aller et le retour est indépendante de la pente.
Vous entrerez ensuite les paramètres correspondant aux caractéristiques de la route et du cycliste, soit:
- le poids du cycliste et du vélo en kg
- le coefficient Cx de pénétration dans l'air
- le coefficient f de résistance au frottement
- la direction du vent par rapport au Nord (soit par exemple 90 si le vent souffle de l'Est, 270 s'il vient de l'Ouest) ainsi que sa force exprimée en km/h
- l'énergie dont le cycliste dispose exprimée en kilojoules. Il se peut que vous vous interrogiez sur cette valeur qui n'est pas très familière en cyclisme alors que la notion de puissance l'est beaucoup plus, grâce notamment aux capteurs de puissance qui envahissent le marché depuis quelques années. En cas d'énergie insuffisante, le calculateur l'indiquera et mettra sa valeur à la valeur minimale pour pouvoir effectuer le parcours. Pour fixer les idées, faire 10 km sur le plat, sans vent et à une vitesse de 20 km à l'heure, très grossièrement, cela nécessite 140 kJoules. Si la pente est de 5%, il faut 540 kJoules.
Le calculateur affichera les résultats suivants:
- la longueur du parcours
- le dénivelé positif
- le dénivelé négatif
- la durée du parcours
- la vitesse moyenne
- la puissance moyenne fournie durant le parcours
Un lien vers un fichier de résultats détaillés, sous le format txt ou csv (Excel) au choix, vous permettra de consulter, pour chaque section, la vitesse réalisée, le temps, l'énergie, la puissance ainsi que les caractéristiques de ces sections: longueur, pente, force du vent effectif. Cela vous permettra notamment de voir quelles sont les sections qui nécessiteront une puissance importante.
|
Calculateur Après avoir rempli les cases blanches, cliquez sur la case dédiée pour effectuer le calcul.Les cases
jaunes contiennent les principaux résultats. |
| Haut de page | Retour accueil |